Identifying Quadratic Functions Concavity
Finding Complex Zeros of a Quadratic Function Graphically
We know that the graph of every quadratic function is a
parabola, which is some variation of the
elementary function y = x^2. If a quadratic function has real zeros , these will
appear graphically as x-intercepts,
which are the points where the parabola intersects the x-axis. However, if the
parabola does
not intersect the x-axis, then the function will have two complex zeros which
are complex conjugates. Of
course, we can find these complex zeros algebraically using the quadratic
formula . It turns out that we
can also find these complex zeros rather easily from the graph.
But first, we need to see how to graphically represent a complex number z = a +
bi. To do this, we
set up a rectangular coordinate system much like the Cartesian coordinate
system, except that we use the
horizontal axis to indicate the real part and the vertical axis to indicate the
imaginary part. We refer to
the horizontal axis as the real axis, which represents the real part of a
complex number, and the vertical
axis as the imaginary axis, which represents the imaginary part. The
resulting 2-dimensional coordinate
system is called the complex plane, or Argand plane. The complex number z
= a + bi can then be
represented as the point (a, b) in the complex plane. The real part, a, gives
the horizontal displacement
of z from the origin, and the imaginary part, b, gives the vertical
displacement. For example, the graph
of 2 + 3i is shown in the figure.
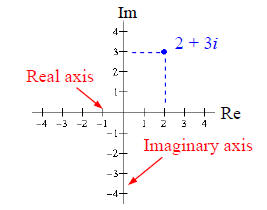
The complex plane is named after the Frenchman
Jean-Robert Argand, who was thought to have
provided the first geometrical interpretation of
complex numbers in 1806. It was discovered 100
years later that the Norwegian-Danish surveyor Caspar
Wessel was actually the first to have done so in a
presentation to the Royal Danish Academy in 1797.
EXERISES
1. Use the quadratic function f(x) = x^2 – 10x + 29 to perform the following.
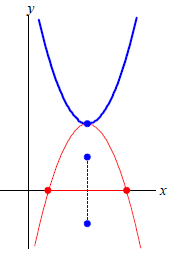
(a) Write the function in vertex form .
(b) Sketch an accurate graph of f using transformations. Show at least 5
points in each step. Also, sketch and label the axis of symmetry.
(c) Notice that the graph of f does not intersect the x-axis, so it has
complex zeros. Find these zeros algebraically.
(d) Reflect the graph of f vertically about its vertex. That is, reflect the
parabola about the line y = k, where k is the y-coordinate of the
vertex. Show at least 5 points on your graph. This new graph will
have the same vertex as f, but will open downward. Call this new
graph g(x).
The graph of g does intersect the x-axis at two points.
Label
these points A and B. Observe that the line segment AB has its midpoint where
the axis of
symmetry crosses the x-axis. Label this midpoint C. Rotate segment AB 90°
clockwise about C.
It should now be vertical and lie along the axis of symmetry. Label the new
endpoints of this
segment A′ and B′.
(e) If we now interpret A′ and B′ as two points in the complex plane, what two
complex numbers
do these points represent? Compare your answer to your results from part (c).
2. Use this method to determine the complex zeros of f(x)
= −2x^2 – 12x – 20. Show at least 5 points on
both of your graphs.
3. Prove that this method works for any quadratic function
whose graph does not intersect the x-axis.
The following steps will help you organize your proof.
(a) Let g(x) = ax^2 + bx + c be any quadratic function with two distinct real
zeros. Write g in vertex
form and express the two zeros in terms of a , b, and c. Since we are assuming
the zeros are
real, what must be true about the quantity b^2 – 4ac?
(b) Find the equation of f (x), whose graph is the reflection of the graph of g
about the line y = k
(where k is the y-coordinate of the vertex of g). Express the zeros of f in
terms of a, b, and c.
Explain why these must be complex numbers, and write them in standard form using
the
imaginary unit i.
(c) Graph the zeros of g and the zeros of f in the complex plane. Show that both
pairs of zeros are
symmetric about the same point on the x-axis. Based on this symmetry, explain
how the zeros
of f are identical to the zeros of g, only rotated 90° in the complex plane.
| Prev | Next |