Math 1033 Intermediate Algebra
I. COURSE DESCRIPTION
Course Title and Number: Mathematics 80
Descriptive Title: Intermediate Algebra for Science, Technology, Engineering,
and Mathematics
Discipline: Mathematics
Division: Mathematical Sciences
Course Length:  Full Term
Full Term
 Other (specify):
Other (specify):
Hours Lecture: 5 Hours Laboratory:___ Course Units: 5
Grading Method: ![]() Letter
Letter
![]() Credit/No Credit
Credit/No Credit
![]() Both
Both
![]() No Grade
No Grade
Course Type: ![]() Credit,
Degree Applicable
Credit,
Degree Applicable ![]() Credit,
Not Degree Applicable
Credit,
Not Degree Applicable ![]() Non-Credit
Non-Credit
Transfer CSU: ![]() Yes
Effective Date______
Yes
Effective Date______ ![]() No
No
Transfer UC: ![]() Yes
Approval Date______
Yes
Approval Date______ ![]() Pending
Pending
![]() No
No
Conditions of Enrollment:
Specify Prerequisite Corequisite , Recommended Preparation, Enrollment Limitation
or None.
Prerequisite: Mathematics 40 or Mathematics 41B with a minimum grade of C in
prerequisite or
qualification by testing (El Camino College Mathematics Placement Test) and
assessment
Catalog Description:
This intermediate algebra course is designed for students who are considering
further study in the
sciences, technology, engineering, or mathematics. In the context of studying a
large library of basic
functions and their graphs, students strengthen and expand their algebra skills.
The library includes
linear, quadratic, polynomial, rational, radical, exponential, and logarithmic
functions, as well as
inverse functions and the absolute value function . Particular emphasis is placed
on the operations on
functions, as well as solving equations and inequalities. Other topics include
solving systems of
equations, operations on complex numbers , and applications.
Note: Mathematics 80 serves as a prerequisite course for all transfer-level
mathematics course
sequences, INCLUDING the calculus sequence (Mathematics 170, 180, 190, 191 and
220). This
intermediate algebra course satisfies the Associate of Arts and Associate of
Science general
education mathematics competency requirement.
II. COURSE OBJECTIVES
List the major objectives of the course. These must be stated in behaviorally
measurable terms.
1. Carry out numerical operations and manipulate algebraic expressions,
including expressions
with rational and negative exponents, complex numbers, and logarithms.
2. Recognize functional relationships in the form of graphs, data or symbolic
equations.
3. Solve problems involving a variety of function types, including linear,
quadratic, polynomial,
rational, radical, exponential, and logarithmic functions.
4. Graph a variety of functions and relations and draw connections between these
graphs and
solutions to problems.
5. Solve a variety of equations and inequalities, as well as systems of
equations and inequalities,
using algebraic and graphical methods. Types of equations include linear,
quadratic,
polynomial, rational, radical, exponential and logarithmic equations.
6. Using numerical, symbolic and graphical methods, model application problems,
solve them
and interpret the results in the context of the problem.
III. OUTLINE OF SUBJECT MATTER
The topics should be detailed enough to enable an instructor to determine the
major areas that should
be covered and so that the course may have consistency from instructor to
instructor and semester to
semester.
| Approximate Time in Hours | Major Topics |
| 13 | Basic Operations and Manipulations: |
| • Review of operations on polynomial, rational
and radical expressions • Operations on exponential and logarithmic expressions, power expressions with negative or rational exponents, as well as absolute value expressions • Factoring polynomial expressions • Rewriting radical expressions as expressions with rational exponents • Properties of exponential and logarithmic expressions • Conversion between logarithmic and exponential statements • Operations on complex numbers |
|
| 18 | Functions: |
|
• Definitions of function, domain and range • Function notation • Functions as rules , as sets of ordered pairs , as algebraic equations, and as graphs. Function types include polynomial, power, rational, radical, exponential, logarithmic and the absolute value • Operations on functions, including addition, subtraction , multiplication, division, exponentiation and composition • One-to-one functions • Inverse functions • Determining the equation for a linear function given the graph or sufficient data |
|
| 19 | Graphing: |
• Graphing functions of all types, especially the
basic functions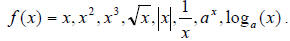 • Graphing
solutions to equations and inequalities |
|
| 21 | Equations and Inequalities: |
| • Algebraic and graphical methods for solving
equations and inequalities • Techniques for solving quadratic equations over the complex numbers • Techniques for solving quadratic inequalities over the real numbers • Techniques for solving other equations and inequalities, which contain polynomial, rational, radical, exponential and logarithmic expressions, as well as the absolute value of linear expressions. • Finding domains of radical, rational and logarithmic functions by setting up and solving appropriate inequalities. • Using interval notation to express solutions of inequalities • Operations on sets: unions and intersections • Systems of linear equations (2 x 2 systems and 3 x 3 systems) |
|
| 19 | Applications |
| • Modeling verbally expressed problems
numerically, symbolically and graphically • Solving problems numerically, symbolically and graphically • Pattern recognition strategies • Perimeter and area of rectangles, triangles and circles • Pythagorean Theorem • Rate, distance and time problems • Exponential growth and decay problems • Other applied problems whose solutions utilize the function types listed above, as well as the types of equations and inequalities listed above • Applied problems whose solutions require the use of systems of linear equations |
|
| Total: 90 hours |
IV . METHODS OF EVALUATION
A. CREDIT, DEGREE APPLICABLE AND CREDIT, NOT DEGREE APPLICABLE COURSES
Check the PRIMARY method of evaluation for this course.
![]() Substantial writing
assignments
Substantial writing
assignments
![]() Problem solving
demonstrations (computational or non-computational)
Problem solving
demonstrations (computational or non-computational)
![]() Skills demonstrations
Skills demonstrations
A minimum of one response in the categories 1, 2, or 3 below, as applicable, is
required.
However, you may check all that apply.
1. Indicate the types of writing assignments used as primary or secondary
methods of
evaluation for this course.
|
|
|
|
|
|
|
|
|
2. Indicate the types of problem-solving demonstrations used as primary or
secondary
methods of evaluation for this course.
|
|
|
|
|
|
|
|
|
3. Indicate the types of skill demonstrations used as primary or secondary
methods of
evaluation for this course.
|
|
|
|
|
|
4. If objective exams are also used, check all that apply.
|
|
|
|
|
|
B. NON-CREDIT COURSE
Indicate the methods of evaluation that will be used to determine that stated
objectives have been
met.
V. COURSEWORK
A. TYPICAL ASSIGNMENT
Provide an example of a typical assignment. This assignment must correspond to
the PRIMARY
method of evaluation indicated in Section IV, Methods of Evaluation. That is, it
must be a writing
assignment or, if more appropriate, an assignment involving problem solving or
skill demonstration.
Solve the inequality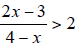 , check your work and
present the solution in interval notation.
, check your work and
present the solution in interval notation.
Also, graph the solution on a number line and on the x-y coordinate plane.
B. COLLEGE-LEVEL CRITICAL THINKING ASSIGNMENTS
Cite two specific assignments that demonstrate college-level critical
thinking. (Required for degree
applicable courses only.)
1. The price of computer technology has been dropping steadily for the past ten
years. If a certain
computer cost $6700 ten years ago and a computer with the same level of
computing power cost
$2200 three years ago, find the rate of decrease in cost of this level of
computing power per year.
Predict what this level of computing power would cost today. Why will this model
stop making
sense at some point in time? Show all of your work.
2. The population of the world in 1960 was about four billion human beings. If
the population is
growing according to the Malthusian model with an annual growth rate of 1.8%,
what does this
model predict the population of the world to be in the year 2000? Find the
actual world population
in the year 2000. Compare your answer with the actual world population in the
year 2000. What
does this tell you about the Malthusian model? Write a paragraph explaining your
reasoning.
C. WORK OUTSIDE OF CLASS
Two hours work outside of class are required for each hour of lecture or
equivalent . Each student in
this course will be required to participate in the following work outside of
class time. Check all that
apply.
![]() Study
Study
![]() Answer questions
Answer questions
![]() Skill practice
Skill practice
![]() Required reading
Required reading
![]() Problem solving
activity
Problem solving
activity
![]() Written work (such as
essay/composition/report/analysis/research)
Written work (such as
essay/composition/report/analysis/research)
![]() Journal (done on a
continuing basis throughout the semester)
Journal (done on a
continuing basis throughout the semester)
![]() Observation of or
participation in an activity related to course content (such as a
Observation of or
participation in an activity related to course content (such as a
theatre event, museum, concert, debate, meeting)
![]() Course is lab only -
minimum required hours satisfied by scheduled lab time
Course is lab only -
minimum required hours satisfied by scheduled lab time
![]() Other (specify)
Other (specify)
VI. INSTRUCTIONAL METHODOLOGY
A. Check all planned instructional activities that apply:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Note: In compliance with Board Policies 1600 and 3410, Title 5 California Code
of Regulations, the
Rehabilitation Act of 1973, and Sections 504 and 508 of the Americans with
Disabilities Act,
instructional delivery shall provide access, full inclusion, and effective
communication for students
with disabilities.
VII. TEXTS AND MATERIALS
If multiple selection is offered, only representative texts need be listed. An
up-to-date list of required
and recommended materials is maintained in the division office.
A. REQUIRED TEXTS (title, author, publisher, year)
Intermediate Algebra, 3rd Edition, A. Tussy and R. Gustafson, Brooks/Cole, 2005
B. REQUIRED SUPPLEMENTARY READINGS
C. OTHER REQUIRED MATERIALS
VIII. CONDITIONS OF ENROLLMENT
If this course has a Prerequisite or Corequisite, complete section A. If this
course has an Enrollment
Limitation complete section B.
A. PREREQUISITE AND/OR COREQUISITE
1. Indicate if this course has a prerequisite or corequisite or both.
![]() Prerequisite
Prerequisite
![]() Corequisite
Corequisite
![]() Both
Both
2. Indicate Type. Check all that apply.
|
|
|
|
|
|
|
|
3. Entrance Skills/Knowledge
List the required skills and/or knowledge without which a student would be
highly unlikely to
receive a grade of A, B, C, or Credit (or for Health and Safety, would endanger
self or others) in
this course.
1. Manipulate algebraic expressions, including expressions with fractions and
radicals.
2. Solve quadratic equations and systems of linear equations.
3. Graph systems of linear equations.
4. Solve application problems using linear and quadratic equations.
B. ENROLLMENT LIMITATION
1. Indicate the category which describes the Enrollment Limitation for this
course.
![]() Band/Orchestra
Band/Orchestra
![]() Theater
Theater
![]() Speech
Speech
![]() Chorus
Chorus
![]() Journalism
Journalism
![]() Dance
Dance
![]() Intercollegiate
Athletics
Intercollegiate
Athletics
![]() Honors Course
Honors Course
![]() Blocks of Courses
Blocks of Courses
![]() Other (specify)
Other (specify)
2. List Degree and/or Certificate requirements that are met by this course.
3. List all El Camino College courses that also satisfy the requirements listed
above in
Section B.2.
Originator: Amy Muneoka Submittal Date: Spring 1977
BOARD APPROVAL DATE:
Reviewed and/or Revised by:
| Marc Glucksman | Date: October, 1987 |
| Susan Taylor | Date: October, 1998 |
| Linda Ho | Date: November, 2001 |
| Robert Lewis | Date: May, 2007 |
REQUIRED SIGNATURES FOR NON-CREDIT COURSE
College Curriculum Committee Chair
Vice-President - Academic Affairs
| Prev | Next |