The Algebra of Functions

Overview of Objectives, students should be able to: 1. Find the domain of the function in equation form a. Find the domain of a linear, quadratic, polynomial, rational, and radical function. b. Find the domain of a square root function c. Find the domain of a rational function 2. Use the algebra of functions to combine functions a. Find the sum function and its domain b. Find the difference function and its domain c. Find the product function and its domain d. Find the quotient function and its domain	Main Overarching Questions: i. What could cause the domain of a function to be restricted? i. When you add, subtract, multiply, or divide functions , how is the domain affected?

Objectives:	Activities and Questions to ask students:
• Find the domain of the function in equation form o Find the domain of a linear, quadratic, polynomial, rational, and radical function. o Find the domain of a square root function o Find the domain of a rational function	Ask students to recall how to determine the domain and range of a relation (look at the x/y values on the table , look at the x/y values from the points on the graph). Because functions are special types of relations, every function also has a domain and a range. Provide a linear function, and then ask students to discuss in pairs how they would determine the domain of that function. Ask individuals to share out responses after a few minutes. (Create a t‐ chart , plot points , etc.) Lead the class in creating a short table of values for the linear function. Ask students, “Would this table represent all of the possible x and y values for this function? How many different numbers could I substitute for x ? How many possible output values are there for y?” Guide students toward understanding that you could plug in an unlimited number of x‐values, so the domain would be unrestricted. Provide the students with the equation for a horizontal line (ex. f(x) = 5). What is the domain for this function? What is the range? Provide a simple quadratic function for students (ex. f(x) = x^2 + 5). Ask students to work in pairs again to determine a method for finding the domain . Have students share their methods with the entire group. Guide students through a similar process as the linear function, creating a table of values and/or graphing. Is there any x‐value that would be invalid as an input for this function? Would this be the case for any quadratic function? Provide a similar example and use a similar process for a polynomial function . Provide an example of a basic rational function (ex. f(x) = 4/(x‐2). Ask students to work in pairs to determine the domain of the function. Ideally, students will recognize a problem when they try to substitute x = 2. Ask students why the error occurred. Can x = 2 in this function? Why not? Discuss the implications for the domains of rational functions. Guide students to the conclusion that any input value that causes the denominator to equal zero should be excluded from the domain of a rational function. Provide several additional examples from whole group or small group practice. Provide an example of a basic radical function (ex. 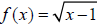). Have students work in pairs to determine the domain of the function. Ideally, students will recognize a problem when they try to input values that are less than 1. Ask students why the error occurred. Discuss the implications for the domains of radical functions. Guide students to the conclusion that any input value that causes the radicand to be negative should be excluded from the domain of a radical function. Provide several additional examples for whole group or small group practice. Briefly review the situations that can create restrictions on the domain of a function (zero in the denominator, negative radicand). Provide a problem set for independent practice. **Possible graphing calculator usage : After students have identified the domains for each of the sample functions above, allow them to graph them in the calculator. Assist them in making connections between the domains and the graphs.

• Use the algebra of functions to combine functions o Find the sum function and its domain o Find the difference function and its domain o Find the product function and its domain o Find the quotient function and its domain	1. Review the terms sum, difference, product and quotient. Solicit student definitions for each. 2. Sometimes it is useful to combine two or more functions into a single function. Given that f(x) = 2x + 1 and g(x) = ‐3x ‐4, how could we simplify f (x) + g(x)? Have students work in pairs to come up with an answer. Ask individuals to share methods with the entire group. 3. What were the domains of the original functions f(x) and g(x)? What is the domain of f(x) + g(x)? 4. Using the same functions, ask pairs to determine the difference and share methods. Emphasize that you are subtracting the entire value of g(x), showing students how to distribute the subtraction sign to each term . 5. Discuss the domain of the difference. Is it any different than the domain of the sum? 6. Using the same functions, ask pairs to determine the product and share their methods with the whole group. Emphasize the fact that each term in the first function must be multiplied by each term in the second function by distributing (you may need to review FOIL and distributive property ). 7. Discuss the domain of the product. Has it changed from the original functions and if so, how? 8. Repeat the process for the quotient of the functions. Discuss changes to the domain, emphasizing that any value that makes the denominator zero should be excluded from the domain. 9. Model additional examples using quadratic, polynomial, radical, and rational functions. For each, ask students to determine the domain of the original functions and the domain of the resulting function. Re‐emphasize that denominators of zero and negative radicands will result in restrictions to the domain. 10. Provide a problem set for independent practice.