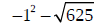Distance and Midpoint
1.1 Distance and Midpoint
Distance Formula – know by heart!
for
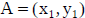 and
and
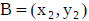
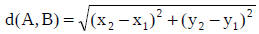
Midpoint formula for a segment with endpoints A and B – know by heart
for
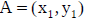 and
and
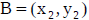
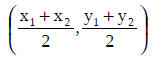
simplify -20
Examples
Given the following points, find the distance between them and the midpoint of
the
segment joining them. Sketch a little graph of the segment being sure to use
appropriate
scaling.
A. ( 1, 2) and ( 5, -3)
Distance
Midpoint
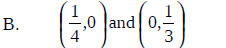 big hint 9(16) = 144
big hint 9(16) = 144
Distance
Midpoint
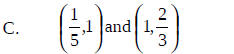 big hint 9(16) + 25 = 169
big hint 9(16) + 25 = 169
Distance
Midpoint
1.2 Lines
Review
Ax + By + C = 0
is the General Equation of a Line
Parts of a line:
x intercept – where the line hits the x axis, y = 0
y intercept – where the line hits the y axis, x = 0
slope – a number that measures incline
Example A:
8x - 2y - 10 = 0
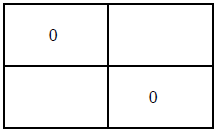
The first row shows the coordinates of the y intercept .
The second row shows the coordinates of the x intercept.
From this we can calculate the slope
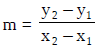
Example B:
6x - 3y - 18 = 0
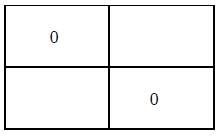
The first row shows the coordinates of the y intercept.
The second row shows the coordinates of the x intercept.
From this we can calculate the slope
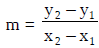
If x = -5 , what is y?
If y = 2/3, what is x?
Let’s calculate some slopes:
Given the following points, find
The slope of the line joining them
The distance between them
The midpoint of the segment joining them
( 2, - 5) and (-3, 10)
Example C:
4x - 8y - 16 = 0
The first row shows the coordinates of the y intercept.
The second row shows the coordinates of the x intercept.
From this we can calculate the slope
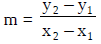
If x = 3/2 , what is y?
If y = 1/4 , what is x?
Now for a bit of review:
Given the line 9x + 3y +18 = 0. Find the following
The slope of the line
The coordinates of the intercepts
The distance between the intercepts
The midpoint of the segment joining the intercepts
If x = -1, what is y?
If y = 2/3, what is x?
Remind me to sketch a graph of this as we go .
| The Slope Intercept form for a line | y = mx + b |
| The slope shows explicitly | m |
| The y intercept is | ( 0, b) |
What is the x intercept?
Example
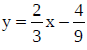
The slope is ________________
The y intercept in coordinate form is ______________________
The x intercept in coordinate form is _____________________
If x = 3/4 , what is y?
If y = 1, what is x?
Point slope equation of a line is:
Using the point slope equation, find an equation of the line through (1, 5) and
(2, 6).
What are the intercepts, the slope, the slopes of all lines perpendicular to
this line?
What is the y coordinate of the point on the line that has x coordinate 3?
What is the x coordinate of the point on the line that has y coordinate -2?
Parallel lines have the same slope and different y intercepts .
Perpendicular lines have slopes that multiply to -1.
What are the slopes of all lines parallel to the line with y intercept 3 that
passes through
(2, -5)? What about all perpendicular lines?
Let’s talk about the points
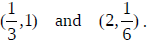
Distance
Midpoint
Equation of line containing them
Slope of all lines parallel
Slope of all lines perpendicular
1.3 Graphing Equations
The x intercept is
to solve for the x intercept (s): 0 = f(x)
The y intercept is
to solve for the y intercept (s): f(0)
evaluation:
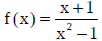
explore:
x = 0
x = -1 or 1
x = 2
solve for the x intercept(s):
The domain is
The range is
Be sure to review evaluation:
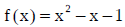
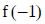
Sample attendance popper questions are on my website.
| Prev | Next |