Get it on Google Play Get it on Apple Store



EXAMPLES OF LINEAR SIMULTANEOUS EQUATIONS PROBLEMS SOLVED BY GAUSSIAN ELIMINATION
Adding,subtracting,multiplying,dividing,integers, linear inequalities absolute value two variable ,     calculator program solving three variable equations ti-83 ,   solving equations algebraically -mutiply or divide, adding\subtracting\multiplying\dividing fractions  
 Thank you for visiting our site! You landed on this page because you entered a search term similar to this: examples of linear simultaneous equations problems solved by gaussian elimination.We have an extensive database of resources on examples of linear simultaneous equations problems solved by gaussian elimination. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!  

More on Linear Systems

Number of Solutions

Most linear systems you will encounter will have exactly one solution.However, it is possible that there are no solutions, or infinitely many.(It is not possible that there are exactly two solutions.)

Let's take a closer look. It never hurts in any investigation to lookat the simplest possible case first. So consider again the singleequation

$\displaystyle ax=b\qquad(*) $

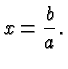
where $ a $ and $ b $ are parameters and $ x $ is the variable whosevalue needs to be determined.There are three possible cases:

  1. $ a\neq 0: $ In this case dividing by $ a $ on both sides of$ (*) $ gives the unique solution

    $\displaystyle x= \frac{b}{a}. $

    The word unique in this context means there is a solution, andit's the only one.

  2. $ a=0 $ and $ b\neq 0 $. In this case $ (*) $ turns into $ 0=0x=b\neq 0 $.Since $ 0\neq 0 $ is impossible there is no solution.

  3. $ a=0 $ and $ b=0 $. In that case $ (*) $ turns into $ 0x=0 $which is true for all numbers $ x $. There are infinitely manysolutions.

It is clear since we cover all possibilities above that it isimpossible for the $ (*) $ to have precisely $ 2 $, or $ 3 $, or anyfinite number, of solutions. Compare this for example with quadratic equations which may have $ 0 $, $ 1 $, or $ 2 $, but neverany other number of (real) solutions.

Next Consider two equations in two unknowns, let's say

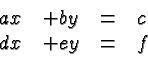
\begin{displaymath}\begin{array}{rrcl}ax & + by &=& c \\dx & + ey &=& f\\\end{array} \end{displaymath}

Each of these two equations defines a line in the cartesian plane . All solutions are the coordinates of a pointwhere the two lines intersect.There are again three possibilities.

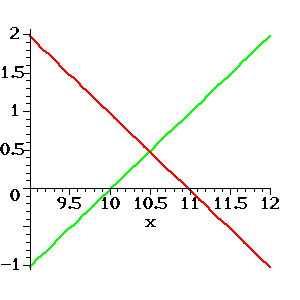
  1. Figure 1: Unique Solution of two equations in two unknowns.

    The lines intersect in one point. There is a unique solution(i..e, the coordinates of that point). An example is provided by

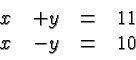
    \begin{displaymath}\begin{array}{rrcl}x & + y &=& 11 \\x & - y &=& 10\\\end{array} \end{displaymath}

    The solution is $ x=10.5 $ and $ y=0.5 $, as shown in Figure 1.

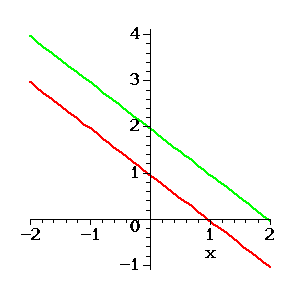
  2. Figure 2: No Solution of two equations in two unknowns.

    The lines are parallel but distinct. They never intersect andthere is no solution.An example is provided by

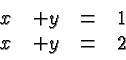
    \begin{displaymath}\begin{array}{rrcl}x & + y &=& 1 \\x & + y &=& 2 \\\end{array} \end{displaymath}

    Note that obviously the two equations contradict each other, nothingcan simultaneously equal $ 1 $ and $ 2 $.

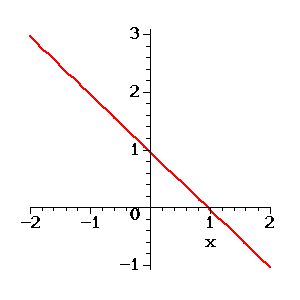
  3. Figure 3: Infinitely many solutions of two equations in two unknowns.

    The lines are identical. Any point on the lines provides asolution. A trivial example can be obtained by writing the sameequation twice. A less trivial example is

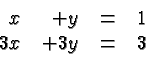
    \begin{displaymath}\begin{array}{rrcl}x & + y &=& 1 \\3x & + 3y &=& 3 \\\end{array} \end{displaymath}

    The second equation follows from the first by multiplying on bothsides with 3.

More than two Equations. Similar considerations apply to systems of more than two equations,but this is a subject beyond the scope of this class. You will learnmore when you take a class on Linear Algebra.

A Complicated Example

Suppose we want to find a quartic polynomial whose value equals$ 2^x $ for $ x=0,1,2,3,4 $. The purpose of this exercise might be toto approximate $ 2^x $ by a polynomial on a calculatorthat cannot evaluate $ 2^x $ for non-integer $ x $ directly.Approximating functions is a huge subject, here we just use thisproblem as an example for a more complicated linear system.

Let's write our quartic polynomial as

$\displaystyle p(x) = e+dx+cx^2+bx^3+ax^4. $

We want it to satisfy the equations

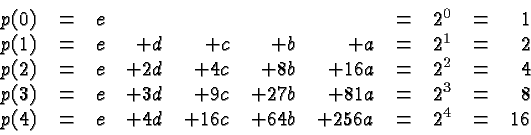
\begin{displaymath}\begin{array}{rcrrrrrcrcr}p(0) & = & e & & & & & = & 2^0 & ...... +4d & +16c & +64b & +256a & = & 2^4 & = & 16 \\\end{array} \end{displaymath}

This is a linear system of five equations in the five unknowns $ a $, $ b $,$ c $, $ d $, and $ e $.

The table below is set up asdiscussed except that whenever an entry is $ 0 $ it is left blankto clarify the reduced systems.

\begin{displaymath}\begin{array}{rrrrrrrrr}\hbox{equation} & & e & d & c & b &......{[15] = [14]-4[13]} & & & & & & 24 & 1 & 25 \\\end{array}\end{displaymath}

Equation $ [1] $ is very special, it tells us right away that $ \underline{e=1} $.We use that equation to eliminate $ e $ from the remaining equationswhich gives us four equations ($ [6] $ through $ [9] $) in the fourunknowns $ a $, $ b $, $ c $ and $ d $.

Equation $ [15] $ is $ 24a=1 $ which means$ \underline{a=\frac{1}{24}} $.Substituting the value of $ a $ into equation $ [13] $ gives $ 36a + 6b= \frac{3}{2} + 6b = 1 $ which implies $ \underline{b =-\frac{1}{12}} $.Substituting $ a $ and $ b $ into equation $ [10] $ gives the equation$ 14a+6b+2c = \frac{7}{12} -{1}{2} + 2c = 1 $ which implies$ \underline{c=\frac{11}{24}} $. Finally, substituting $ a $, $ b $and $ c $ into equation $ [6] $ gives$ a+b+c+d = \frac{1}{24} -\frac{1}{12} + \frac{11}{24}+d=1 $ whichimplies $ \underline{d=\frac{7}{12}} $.

Putting the underlined results together (and writing everything overthe common denominator $ 24 $) gives

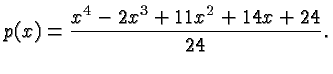
$\displaystyle p(x) = \frac{x^4-2x^3+11x^2+14x+24}{24}. $

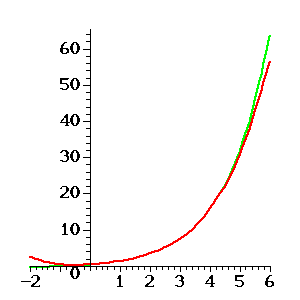
Figure 4: A polynomial approximation of $ f(x) = 2^x $.

Figure 4 shows the graph of $ p $ (red) as well as the graphof $ f(x) = 2^x $ (green). It is apparent that $ p $ is a good approximation of $ f $ in the interval from $ 0 $ to $ 5 $. There are other andmore effective ways of computing polynomials like $ p $. However,this example illustrates how Gaussian Elimination and BackwardSubstitution can be used to solve a linear system. In this particularlinear system we were fortunate in that the elimination proceeded in astraightforward way without fractional arithmetic. It happensfrequently that linear systems have a special structure that can beeffectively exploited.

A final word on computing the row sums. They appear to be a waste ofeffort when the problem is all solved. However, when I first computedthe entries in the above table I made several mistakes that Idiscovered immediately because of the row sums. There is a goodchance you will save yourself a lot of time and aggravation bycarrying them along in your own calculations.