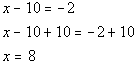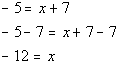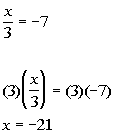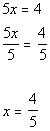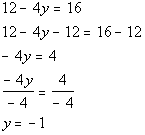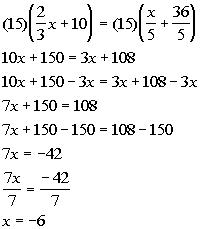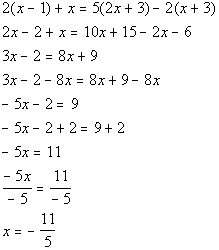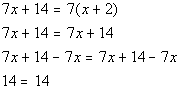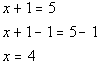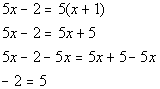College Algebra
Tutorial 14:
Linear Equations in OneVariable
 Learning Objectives Learning Objectives |
After completing this tutorial, you should be able to: - Know what a linear equation is.
- Know if a value is a solution or not.
- Use the addition, subtraction, multiplication, anddivision propertiesof equalities to solve linear equations.
- Classify an equation as an identity, conditional orinconsistent.
|
 Introduction Introduction |
| This is where we start getting into the heart of whatalgebra is about- solving equations. In this tutorial we will be lookingspecificallyat linear equations and their solutions. We will start off slowandsolve equations that use only one property to make sure you have theindividualconcepts down. Then we will pick up the pace and mix 'em up whereyou need to use several properties and steps to get the job done. Equations can be used to help us solve a variety ofproblems. In latertutorials, we will put them to use to solve word problems. |
 Tutorial Tutorial |
| Equation Two expressions set equal to each other |
| Linear Equation An equation that can be written in the form
ax + b = 0
where a and b are constants |
| Note that the exponent (definitionfound in Tutorial 2: Integer Exponents) on the variable of a linearequation is always 1. |
| The following is an example of a linear equation: 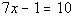
|
| Solution A value, such that, when you replace the variable withit, it makesthe equation true. (the left side comes out equal to the right side) |
| Solution Set Set of all solutions |
Solving a Linear Equation
in General Get the variable you are solving for alone on one sideand everythingelse on the other side using INVERSE operations. |
| The following will give us the tools that we need tosolve linear equations. |
| Addition and SubtractionProperties of Equality If a = b, then a + c = b + c If a = b, then a - c = b - c |
| In other words, if two expressions are equal to eachother and youadd or subtract the exact same thing to both sides, the two sides willremain equal. Note that addition and subtraction are inverseoperations of eachother. For example, if you have a number that is being added thatyou need to move to the other side of the equation, then you wouldsubtractit from both sides of that equation.
 Example1: Solve Example1: Solve 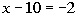 for x. for x.
|
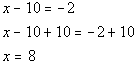 | *Inverse of sub. 10 is add.10 |
| Note that if you put 8 back in for x inthe original problem you will see that 8 is the solution to ourproblem. |
 Example2: Solve Example2: Solve 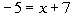 for x. for x. |
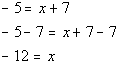 | *Inverse of add. 7 is sub. 7 |
| Note that if you put -12 back in for xin the original problem you will see that -12 is the solution wearelooking for. |
| Multiplication and DivisionProperties of Equality If a = b, then a(c) = b(c) If a = b, then a/c = b/c where c isnot equal to 0. |
| In other words, if two expressions are equal toeach other and youmultiply or divide (except for 0) the exact same constant to bothsides,the two sides will remain equal. Note that multiplication and division are inverseoperations of eachother. For example, if you have a number that is being multipliedthat you need to move to the other side of the equation, then you woulddivide it from both sides of that equation. Note, for multiplication and division, it is notguaranteed that ifyou multiply by the variable you are solving for that the two sides aregoing to be equal. But it is guaranteed that the two sides aregoingto be equal if you are multiplying or dividing by a constant or anothervariable that you are not solving for. We will talk more aboutthisin a later tutorial. For this tutorial just note you can use thisproperty with constants and variables you are not solving for.
 Example3: Solve Example3: Solve 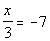 for x. for x.
|
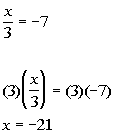 | *Inverse of div. by 3 is mult.by 3 |
| If you put -21 back in for x inthe originalproblem, you will see that -21 is the solution we are looking for. |
 Example4: Solve Example4: Solve 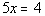 for x. for x. |
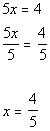 |
*Inverse of mult. by 5 is div. by 5
|
| If you put 4/5 back in for xin the originalproblem, you will see that 4/5 is the solution we are looking for. |
| The examples above were usingonly one propertyat a time to help you understand the different properties that we usetosolve equations. However, most times, we have to use severalpropertiesto get the job done. The following is a strategy that you can useto help you solve linear equations that are a little bit more involved. |
| Strategy for Solving a LinearEquation |
Note that your teacher or thebook you areusing may have worded these steps a little differently than I do, butitall boils down to the same concept - get your variable ononeside and everything else on the other using inverse operations.
Step 1:Simplify eachside, if needed.
| This would involve things like removing ( ),removing fractions, addinglike terms, etc. To remove ( ): Just use thedistributive property. To remove fractions: Since fractions areanother way to writedivision, and the inverse of divide is to multiply, you removefractionsby multiplying both sides by the LCD of all of your fractions. | Step 2:Use Add./Sub.Properties to move the variable term to one side and all other terms tothe other side.
Step 3: UseMult./Div.Properties to remove any values that are in front of the variable.
Step 4: Check youranswer.
I find this is the quickest andeasiest wayto approach linear equations.
 Example5: Solve Example5: Solve 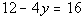 for y. for y.
|
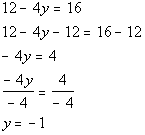 | *Inverse of add. 12 is sub. 12
*Inverse of mult. by -4 is div.by -4
|
| Be careful going from line 4to line 5. Yes, there is a negative sign. But, the operation between the -4 and xis multiplication not subtraction. So if you were toadd4 to both sides you would have ended up with -4x+ 4 instead of the desired x. If you put -1 back in for yin the originalproblem you will see that -1 is the solution we are looking for. |
 Example6: Solve Example6: Solve 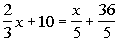 for x. for x. |
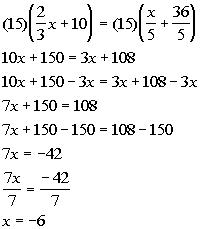 | *To get rid of thoseyucky fractions,
mult. both sides by the LCD of 15
*Get all the xterms on one side
*Inverse of add. 150 is sub. 150
*Inverse of mult. by 7 is div.by 7 |
| If you put -6 back in for xin the originalproblem you will see that -6 is the solution we are looking for. |
 Example7: Solve Example7: Solve 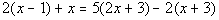 for x. for x. |
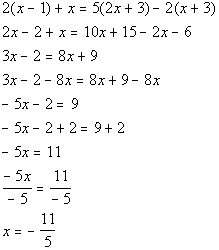 |
*Remove ( ) by using dist. prop.
*Get all xtermson one side *Inverse of sub. 2 is add. 2
*Inverse of mult. by -5 is div.by -5
|
| If you put -11/5 back in for x inthe originalproblem you will see that -11/5 is the solution we are looking for. |
| Identity An equation is classified as an identity when it is truefor ALL real numbers for which both sides of the equation are defined. |
 Example8: Solve Example8: Solve 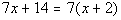 for x. for x. |
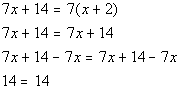 |
*Remove ( ) by using dist. prop. *Get all the xterms on one side
|
| Where did our variable, x,go??? It disappeared on us. Also note how we ended up with a TRUEstatement,14 does indeed equal 14. This does not mean that x= 14. Whenever your variable dropsout AND you endup with a TRUE statement, then the solution is ALL REAL NUMBERS. Thismeans that if you plug in any real number for xin this equation, the left side will equal the right side.
Also note that in line 2 above,both sides of the equation have the same expression. This isanother sign that this equation is an identity.
So the answer is all real numbers, which means thisequation is anidentity. |
| Conditional Equation A conditional equation is an equation that is not anidentity, but hasat least one real number solution. |
 Example9: Solve Example9: Solve 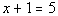 for x. for x. |
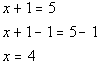 |
*Inverse of add. 1 is sub. 1 |
| If you put 4 back in for x inthe originalproblem you will see that 4 is the solution we are looking for. This would be an example of a conditional equation,because we cameup with one solution. |
| Inconsistent Equation An inconsistent equation is an equation with onevariable that has nosolution. |
 Example10: Solve Example10: Solve 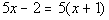 for x. for x. |
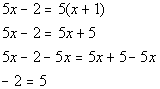 |
*Remove ( ) by using dist. prop. *Get all the xterms on one side
|
| Where did our variable, x,go??? It disappeared on us. Also note how we ended up with a FALSEstatement,-2 is not equal to 5. This does not mean that x= -2 or x = 5. Whenever your variable dropsout AND you endup with a FALSE statement, then after all of your hard work, there isNOSOLUTION. So, the answer is no solution which means this is aninconsistentequation. |
 Practice Problems Practice Problems |
| These are practice problems to help bring you to thenext level. It will allow you to check and see if you have an understanding ofthesetypes of problems. Math works just likeanythingelse, if you want to get good at it, then you need to practiceit. Even the best athletes and musicians had help along the way and lots ofpractice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice. To get the most out of these, you should work theproblem out onyour own and then check your answer by clicking on the link for theanswer/discussionfor that problem. At the link you will find the answeras well as any steps that went into finding that answer. |
 PracticeProblems 1a - 1c: PracticeProblems 1a - 1c: Solve the given equation. |
1a. 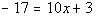
(answer/discussionto 1a) | 1b. 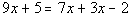
(answer/discussionto 1b) |
1c. 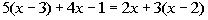
(answer/discussionto 1c) |
 PracticeProblems 2a - 2c: PracticeProblems 2a - 2c: Determine whether the equation is anidentity, a conditionalequation or an inconsistent equation. |
2a. 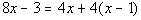
(answer/discussionto 2a) | 2b. 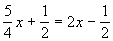
(answer/discussionto 2b) |
2c. 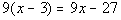
(answer/discussionto 2c) |
 Need Extra Help on These Topics? Need Extra Help on These Topics? |
The following are webpagesthat can assistyou in the topics that were covered on this page:
int_alg_tut7_lineq.htm
This website helps you to solve linear equations in one variable.
This webpage helps you to solve linear equations.
This website helps you solve linear equations using either the additionor subtraction properties of equality.
This website helps you solve linear equations using the divisionpropertyof equality.
This website helps you solve linear equations using the multiplicationproperty of equality.
This webpage gives an example of solving a linear equation.
This website helps you to solve linear equations. Onlydo the linear equations at this site. Do not go on to equationscontainingradicals - that will be covered in a later tutorial. |
forsomemore suggestions. |
All contents
December 29, 2003 |
 Example1: Solve
Example1: Solve