Homework of advanced Algebra
18.02 Notes, Exercices and Solutions are for sale at the Copy
Technology
Center in the basement of Building 11. This is where to find the exercices
labelled 1A, 1B, etc. Problem Sets have two parts , A and B.
Part A has problems from the text, with answers to many in the back of
the text, and problems from the Notes with solutions at the end of the Notes.
Look at the solutions if you get stuck, but try to do as much as possible
without
them. Part A will be graded quickly, checking that the problems are there and
the solutions not merely copied.
Part B consists of unsolved problems, is worth more points, and will
be
graded more carefully. Many of these problems are longer multi-part exercises
posed here because they do not fit conveniently into an exam or short-answer
format.
Collaboration on problem sets is encouraged, but
1. Attempt each part of each problem yourself. Read each portion of
the problem before asking for help. If you dont understand what is being
asked, ask for help interpreting the problem and then make an honest
attempt to solve it .
2. Write up each problem independently. On both Part A and B exercises
you are expected to write the answer in your own words.
3. Write on your problem set whom you consulted and the sources
you used. If you fail to do so, you may be charged with plagiarism and
subject to serious penalties.
4. It is illegal to consult materials from previous semesters .
Reading
The material for this problem set is covered in sections D and M of the 18.02
Notes, Exercises and Solutions, and sections 17.3, 18.1, 18.2, 18.3, 18.4 of
Simmons,
Calculus with Analytic Geometry, 2nd Edition.
Part A (10 points)
Exercises from the Supplementary Notes and Exercises (20 problems, 1/2 point each):
• Vectors (1A): 1A-1, 1A-2, 1A-3, 1A-5,
• Dot Product (1B): 1B-1, 1B-2, 1B-4, 1B-7,
• Determinants (1C): 1C-1, 1C-2, 1C-3,
• Cross Product (1D): 1D-1, 1D-2, 1D-3,
• Equations of Lines and Planes (1E): 1E-1,
• Matrix Algebra (1F): 1F-3, 1F-4,
• Solving Square systems ; Inverse Matrices (1G): 1G-1,
• Cramer’s Rule; Theorems about Square Systems (1H): 1H-3, 1H-5
Part B (25 points)
There are 5 problems worth 5 points each
1. (5 points) Label the four vertices of a parallelogram in counterclockwise
order as OPQR . Prove that the line segment from O to the midpoint of
PQ intersects the diagonal PR in a point X that is 1/3 of the way from P
to R. (Hint: Let
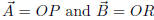 ,
and express everything in terms
,
and express everything in terms
of
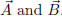 )
)
2. (5 points) The Cauchy-Schwarz inequality
(a) Prove from the geometric definition of the dot product the following
inequality for vectors in the plane or in space:

Under what circumstances does equality hold?
(b) If the vectors are plane vectors, what does this inequality say in terms
of the components of
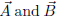 along the
along the 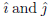 vectors? If the vectors
vectors? If the vectors
are space vectors, what does it say in terms of the components of
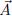
and
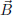 along the vectors
along the vectors
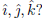
(c) Give a different proof of this inequality by considering, for fixed
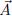
and
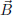 ,
the function
,
the function
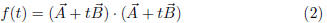
(Hint: First, use the algebraic properties of dot product to write f
as a quadratic polynomial in t . Show that f(t) is never negative.
Thus f(t) can have at most one zero. The quadratic formula implies
that the coefficients of a quadratic polynomial with at most one zero
satisfy a certain inequality.)
3. (5 points) Using vector methods , show that the general formula for the
distance from a point (x0, y0, z0) to the plane defined by the equation

is

4. (5 points) Consider the matrix
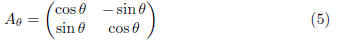
(a) What happens when a vector is multiplied by
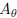 that is, what is
that is, what is
the geometric relationship between a plane vector
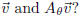 Draw
Draw
a picture showing the two cases 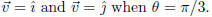
(b) Consider 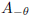 , the same
matrix as (5) but with −θ in place of θ. Compute
, the same
matrix as (5) but with −θ in place of θ. Compute
the matrix multiplication 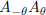 algebraically.
Deduce immediately
algebraically.
Deduce immediately
(without further calculation ) a formula for the inverse matrix
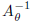 . What is a geometric justification for your
conclusion?
. What is a geometric justification for your
conclusion?
(c) Use trigonometric identities and matrix multiplication
to show that
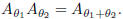 What is a geometric justification for this
identity?
What is a geometric justification for this
identity?
5. (5 points) Suppose that A is a matrix with determinant
zero: |A| = 0,
and that 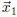 is a solution of
is a solution of
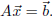 Show that any other solution of this
Show that any other solution of this
system may be written as 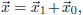 where
where
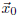 is a solution of the system
is a solution of the system
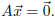
Apply this principle in the particular case of the system
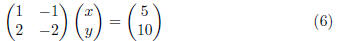
to find a general formula for all solutions of this system (6).
| Prev | Next |