A square root of a number is a number that you can square to get it, that is a number that you can multiply by itself to get the number. So 2 is a square root of 4, because 2²=4 and 3 is a square root of 9, because 3²=9. (-2)² is also 4 and (-3)² is also 9. Numbers that have square roots always have two, a positive one and a negative one. But the square root symbol means only the positive one, so we can have one answer to our problem. Negative numbers don't have square roots, because when you multiply numbers with like signs you get positive numbers.

What about a number like 2 or 5 or 10. Do they have square roots? Are there numbers that you can multiply by themselves to get numbers like these? Clearly there are no whole numbers that will work, but what about something involving fractions? It turns out that fractions won't work either. It turns out that if you can't find a whole number to square and get a given whole number, no fraction will work either. But it also turns out that square roots of all whole numbers do correspond to lengths. This is kind of strange I think, lengths that can't be measured by whole numbers or fractions, but it really is true. To measure such lengths mathematicians use irrational numbers. Read my article Irrational Numbers to learn more about this. You can also find out more about irrational numbers by going on my pi tour.

You can approximate such square roots by rational numbers, and you can get as close as you want, and it is quite easy to do so. The simplest way is to just do a lot of guessing and checking. First find the two whole numbers that it is between and then the nearest 10th, the nearest 100th, etc., etc.. For example if you want to find out what the square root of 2 is, you know that it must be between 1 and 2, because 1²=1 and 2²=4 and 2 is between 1 and 4. 2 is closer to 1 than to 4, so the square root of 2 must be closer to 1 than to 3, but not that much, so we might guess 1.3 or 1.4. If we guess 1.3 and square it we get 1.3²=1.69, which is much too small, so try 1.4. 1.4²=1.96, still too small, but 1.5²=1.25, which is much too big, so to the nearest 10th the square root of 2 is 1.4. To get another decimal space since 1.4²=1.96 is much closer than 1.5²=2.25, we might try 1.41. 1.41²=1.9881, still too small. 1.42²=2.0164, too big. 1.41² is closer, so to the nearest 100th the square root of 2 is 1.41. Continuing like this we should be able to get as close as we want. There are also fancier methods that do it a bit quicker and your calculator uses one of these, and by using a calculator you don't actually have to go through such a long process to find a square root. But it is useful to try it at least once, just to make sure you really know what a square root is. After that you can find an approximation for any square root just by keying the number into the calculator and pushing the square root button.

But since these will only be approximations anyway, most of the time in mathematics we just leave the square root undone and use

as the name for the exact real number that you can square and get 2 in the same way that we use 1/3 to designate the number you get when you divide 1 by 3 and don't always divide it out.

One thing that is important to do is to get using to using radical notation. That funny symbol over the 2 is called a radical. When it is put around a number the whole thing then means the positive number that can be square to get that number. That means, for example, that  means the positive number that you can square and get 4, which means that it is equal to 2. Similarly an expression like

means we are adding the number we can square to get 4 to the number we can square to get 9. The number we can square to get 4 is 2 and the number we can square to get 9 is 3, so this would simplify to 2+3=5, by simply replacing things with what they are equal to. One thing never do is leave the radical there after you have done it. For example would mean that the number you square to get 4 is the same as the number you square to get 2, which is total nonsense. That is why I have crossed it out in red, because I want to make sure you realize that this is wrong. The radical symbol shouldn't be used like the long division symbol. The long division symbol stays around when the division has already been done, because it is not so much a symbol for the operation as a computational tool for keeping track of the division similar to the line separating things that you are adding, subtracting, or multiplying from the answer. In this sense the radical symbol is more like the ÷ symbol, so saying something like the above would be sort of like saying 14÷2=7÷2.

Whenever you have an expression with radicals in it and they can be evaluated, all you have to do to simplify the expression is replace the radicals with what they are equal to. So for example if you have

the square root of 9 is 3, so we replace it with 3, and the square root of 25 is 5, so we replace that with 5, and we get

(5)(3)+(2)(5).

Then we do the rest of the arithmetic and get

15+10=25.

On the other hand, the radical symbol creates an automatic grouping. Any operation inside it is done before taking the square root. So in

you don't find the square root of 4 and the square root of 9 and add them together. Instead it means that you add the 4 and the 9 first, and get 13 and then try to find a number that you can square to get 13. In this case since there is no rational number that you can do that with, the answer would be just . The above kind of simplifying just depends on knowing what the notation means, but there is some additional simplifying of radical expressions that you can do by using a couple of properties. Here are the properties that you need to know for this. The first of these is helpful for writing irrational radicals with as small as possible numbers left inside the radical. The idea is that if you have something like

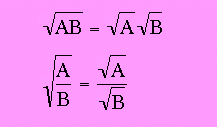
even though you can only approximate the answer to it with a rational number, you can evaluate part of it and make the irrational part smaller, and it is considered to be a simpler way to write it. What you do is you use the first of the properties above to write it as the square root of 4 times the square root of 3, and the important thing here is that the square root of 4 can be evaluated.

Again just like before all I am doing here after I apply the property is replacing things with what they are equal to. When you do this it doesn't do to factor it any way. It is important to factor it so that one of the factors is a perfect square so that you can evaluate it. Sometimes when doing this if you have trouble finding a factor that is a perfect square a good method is to prime factor the number. Then all of the pairs will be perfect squares. In the first radical here you are asking yourself what can you multiply by itself to get 2 times 2, and of course the answer is 2. In the second radical you are asking yourself what can you multiply by itself to get 3 times 3, and of course it is 3. In the third radical you are asking what can you multiply by itself to get 3, and the answer isn't so obvious, because it is a nasty irrational number, so it is best to leave it undone and use the square root of 3 as a symbol for it. Again this is replacing things with what they are equal to. In the last step you multiply the 2 and the 3 to get the final answer.

The second of these properties is useful for evaluating square roots of fractions, because it allows you to do it by finding the square roots of the numerator and the denominator individually.

You could also do this problem by asking yourself what can you multiply by itself to get 4/9 and thinking about how fractions multiply, but it makes it a little easier this way.

It is really important when using these properties to realize that these properties are special to multiplication and division. The reason they work has to do with the fact that powers are repeated multiplication. Powers aren't repeated addition, so there are no similar properties for addition and subtraction. The expression

means you are trying to find the number you can square to get the answer to 9+16. That means you are trying to find the number you can square to get 25. That is 5. On the other hand the expression means you are find the number you can square get 9 and the number you can square to get 16 and you are then adding them together. The number you can square to get 9 is 3. The number you can square to get 16 is 4. The answer then is 3+4=7. 5 and 7 are not equal.