Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solved examples of trigonometric addition and subtraction formulas, here's the result:
Section 5.5: Solving Trigonometric Equations
Now that we have a firm grasp of trigonometric functions algebraically and graphically, we move on to discuss solving equations involving trigonometric functions. This will be useful in the next section when we look at some concrete applications of trigonometric functions to geometry. As we have seen, solving equations generally involves applying inverse functions, so we will be led to discuss the "inverse" trigonometric functions.
Inverse Trigonometric Functions
If you look on your calculator, you may see buttons labeled, sin-1, cos-1, and tan-1. If you think about it, you should realize that none of these trigonometric functions are actually invertible, since they take an (infinite) number of inputs to the same output! That is, this notation is a bit deceptive, but it is not difficult to explain.
To illustrate, you should first notice that the square root function, , is not really the inverse of the square function, f(x) = x2:
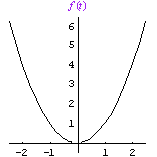
but rather the inverse of the restricted square function, F(x) = x2, if x 0:
.
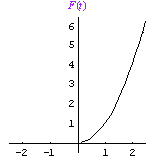By restricting the domain to positive numbers, we have eliminated duplicate values, and have a truly invertible function with inverse F - 1 ( x ) = x "> . However, this means that when apply the square root function to solve an equation, such as:
4 = f(x) = x2 4 = x ">
we will not obtain all possible solutions. But we can use the symmetry of f to write all solutions to 4 = f(x) = x2, in terms of F - 1 ( x ) = x "> :
± 4 = x ">
In the same way, when we talk about the "inverse" trigonometric functions, we are really talking about the inverse of appropriately chosen restrictions of the trigonometric functions. For example, sin-1 is the inverse of the restricted sin function, Sin(x) = sin(x), if -p/2 x p/2:
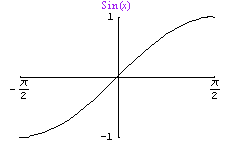
That is, we should really write Sin-1, instead of sin-1. Note: While some textbooks are very careful about this distinction, mathematicians have gotten into the habit of being rather sloppy about this, and simply write sin-1; now that we have explained how this is an abuse of notation, we will be "sloppy", too.
As with the square function, we must be careful when solving, say, 0.5 = sin(x), for x. We can visualize this as those x values where the line y = 0.5 intersects the graph of y = sin(x):
If we simply apply sin-1 to both sides of the equation, we will not obtain all solutions (which would include p/6, 5p/6, 13p/6, -7p/6, etc.); we will only get the one solution x = sin-1(0.5) = p/6 that is between -p/2 and p/2. However, if we examine all solutions visible from the graph, we can see that they fall into two groups:
x = ..., -11p/6, p/6, 13p/6, ...
and
x = ..., -7p/6, 5p/6, 17p/6, ...
Notice how successive solutions in each group are 2p units apart, stemming from the periodicity of the sin function. Notice also that the "smallest" solutions in each group are p/6 and 5p/6 = p - p/6. This suggests that we can conveniently express all solutions in terms of sin-1(0.5) = p/6, as x = 2kp + p/6, (2k + 1)p - p/6, as k runs over all the integers.
In general:
If -1 y 1, the set of all solutions to y = sin(x) is x = 2kp + sin-1(y), (2k + 1)p - sin-1(y), where k can be any integer; that is all even multiples of p plus sin-1(y), together with all odd multiples of p minus sin-1(y). If -1 > y or y > 1, there are no solutions to y = sin(x).
Note: Practically speaking, one does not need to remember the restriction that -1 y 1, since, if -1 > y or y > 1, your calculator will remind you that sin-1(y) is undefined.
We may verify that these all are solutions using the sum and difference formulas for sin:
sin(2kp
+ sin-1(y)) = sin(2kp)cos(sin-1(y))
+ cos(2kp)sin(sin-1(y)) =
0cos(sin-1(y)) + 1y = y
sin((2k + 1)p - sin-1(y)) = sin((2k + 1)p)cos(sin-1(y)) - cos((2k + 1)p)sin(sin-1(y))
= 0cos(sin-1(y)) - (-1)y = y
In the same way, cos-1 is the inverse of the restricted cos function, Cos(x) = cos(x), if 0 x p:
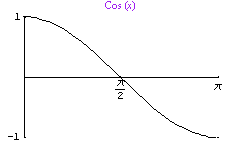
and tan-1 is the inverse of the restricted tan function, Tan(x) = tan(x), if -p/2 < x < p/2:
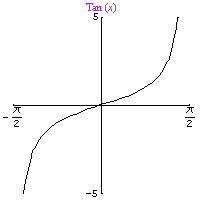
We can use similar graphical and algebraic arguments to show that the corresponding formulas for cos-1 and tan-1 are similar, but even easier:
If -1 y 1, the set of all solutions to y = cos(x) is x = 2kp cos-1(y), where k can be any integer; if -1 > y or y > 1, there are no solutions to y = cos(x).
The set of all solutions to y = tan(x) is x = kp + tan-1(y), where k can be any integer.
As with sin-1, cos-1(y) is undefined, if -1 > y or y > 1, as your calculator should tell you when you try to use the formula.
Practice using these formulas to solve trigonometric equations by
completing the following Exercises.
Solving Trigonometric Equations
To illustrate how to use these formulas in solving trigonometric equations, we will first look at how we would solve an equation such as 1 = -1 + 4(-2x + 3)2:
-
Add 1 to both sides: 1 + 1 = -1 + 4(-2x + 3)2 + 1 so 2 = 4(-2x + 3)2.
-
Divide both sides by 4: 2/4 = 4(-2x + 3)2/4 so 1/2 = (-2x + 3)2.
-
"Take square roots of both sides": 1 2 = - 2 x + 3 "> .
Notice that at this step we did not simply apply the square root function to both sides, but rather we wrote down all solutions to the equation f(t) = 1/2, using the square root function, i.e., as F ( 1 2 ) = 1 2 "> . We then solve this as usual:
-
Subtract 3 from both sides: 1 2 - 3 = - 2 x + 3 - 3 "> so 1 2 - 3 = - 2 x "> .
-
Divide both sides by -2: 1 2 - 3 - 2 = - 2 x - 2 "> so x = 3 1 2 2 ≈ 1.85355 or 1.14645 "> .
We can follow the same procedure to solve a trigonometric equation, such as 1 = -1 + 4sin(-2x + 3):
-
Add 1 to both sides: 1 + 1 = -1 + 4sin(-2x + 3) + 1 so 2 = 4sin(-2x + 3).
-
Divide both sides by 4: 2/4 = 4sin(-2x + 3)/4 so 1/2 = sin(-2x + 3).
-
"Apply sin-1 to both sides" to obtain: 2kp + sin-1(1/2) = -2x + 3 or (2k + 1)p - sin-1(1/2) = -2x + 3.
Again, we did not simply apply the inverse function, but rather, we used the formula for solutions of the sin function. Since sin-1(1/2) = p/6 , we can simplify and finish, as before:
-
Subtract 3 from both sides: so -2x = 2kp + p/6 - 3 or (2k + 1)p - p/6 - 3.
-
Divide both sides by -2: so x = (2kp + p/6 - 3)/(-2) or ((2k + 1)p - p/6 - 3)/(-2).
which simplifies to x = 3/2 - p/12 - kp or 3/2 - 5p/12 - kp. This gives an algebraic description of the infinite number of solutions to our original equation.
Plugging these expressions into a calculator, for different values of k, gives numerical values for all the solutions, such as x ..., 4.37979, 3.3326, 1.2382, 0.191003, -1.90339, -2.95059, .... Note: These are the values for the two expressions for k = -1, 0, 1. If were were interested in a particular solution, such as the smallest solution greater than 5, we can simply estimate an appropriate value for k, which in this case would probably be around -2, and plug in. For example, since the two expressions give x 7.52139, 6.47419, 4.37979, 3.3326 when k = -2 or -1, we can see that the desired solution is x = 3/2 - 5p/12 - (-2)p = 3/2 + 19p/12 6.47419.
This example was a bit special, in that we could solve exactly for sin-1(1/2). In general, we will only be able to obtain approximate solutions, since we will need to rely on our calculator for the necessary value of the appropriate inverse trigonometric function. For example, to solve -6 = -1 + 4tan(-2x + 3):
-
Add 1 to both sides: -6 + 1 = -1 + 4tan(-2x + 3) + 1 so -5 = 4tan(-2x + 3).
-
Divide both sides by 4: -5/4 = 4tan(-2x + 3)/4 so -1.25 = tan(-2x + 3).
-
Use the formula for solutions of the tan function to obtain: kp + tan-1(1.25) = -2x + 3.
-
Subtract 3 from both sides: so -2x = kp + tan-1(1.25) - 3.
-
Divide both sides by -2: so x = (kp + tan-1(1.25) - 3)/(-2) or 3/2 - kp/2 - tan-1(1.25)/2.
This is an exact, algebraic description of all solutions to our original equation. Plugging this into a calculator gives values, such as x ..., 2.17474, 0.603945, -0.966852, .... , when k = ..., -1, 0, -1, ....
Practice solving trigonometric equations by completing
the following Exercises.