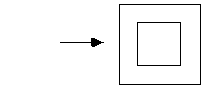
We will work with aformal system based on one symbol, a rectangle.

An expression in this system is a finite collection of non-overlappingrectangles in the plane. For example:

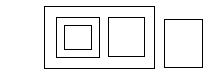
In an expression, one can say about any two rectangles whetherone is inside or outside of the other.

We allow two rules of transformation on expressions.

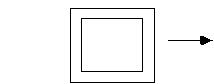
1.Cancellation. Two nested rectangles with the inner rectangle empty and thespace between the two rectangles empty, can be replaced by the absence of the tworectangles. That is they can be erased.

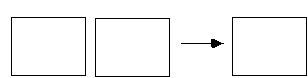
2. Condensation. Two empty adjacent rectangles can be replaced by oneof them.

Proposition. Any finite expression in rectangles can be reduced by aseries of applications of cancellation and condensation to either a singlerectangle or to an empty plane.

Example.

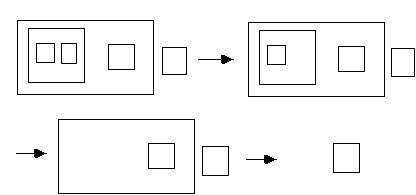
The Problem: Write a proof of this proposition. Your proof should beclearly worded and it should explain why the hypothesis of finiteness forexpressions is needed.

Hints: It is useful to use a concept of depth in an expression. I havelabeled the spaces in the expression below by their depth. The depth of a spaceis the number of inward crossings needed to reach it.

There must be rectangles enclosing spaces of maximal depth in the expression.Such rectangles are empty (else they would not be deepest). Call such a rectanglea deepest rectangle. Now you should be able to show that a deepest rectangleeither has an empty rectangle next to it (so that condensation is possible), orit is surrounded by a rectangle forming a nest of two rectangles (so cancellationis possible), or the deepest rectangle is the only rectangle in the expression.These remarks will provide an algorithm for reducing any given expression toeither a rectangle or to an empty plane.

Further Work: If you are interested you can carry this theory furtherin the following ways.

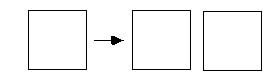
1. Allow the opposite of condensation and cancellation in expressions.That is, allow creation and expansion where expansion allows youto put a new empty rectangle next to an empty rectangle, and creation allows youto create a nest of two rectangles in any empty space.

(a) Creation.

(b) Expansion.

For example:

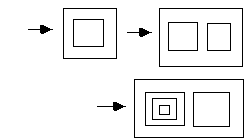
Note that in this example we used only creation and expansion.

Also, itshould be apparent by now that we only care about the relationships of therectangles not their sizes.

Another example. We can use combinations of creation, cancellation,expansion and condensation together.

We shall call two expressions equivalent if one can be obtained from anotherby a finite sequence of these moves (creation, cancellation, expansion andcondensation).

We have shown that any expression is equivalent to either a rectangle or tothe empty plane.

Problem. Show that the rectangle and the empty plane are not equivalentto one another.

Once you have shown this, it follows that the simplification of an expressionto rectangle or empty plane is unique. We will call the

singlerectangle the marked state and the empty plane the unmarked state. Thus everyexpression is equivalent to either the marked state or the unmarked state.

Hint: Find an independent way to evaluate an expression as marked or asunmarked, and then show that your method of evaluation does not change under theelementary equivalences of creation, cancellation, expansion andcondensation.

2. One can then make an algebra in relation to this arithmetic just aswe make algebra in relation to ordinary arithmetic. Given any expressions A andB, we let AB denote their juxtaposition in the plane. We let denote the result of putting a box around the expression A. Since each expression A or B represents either a marked or anunmarked value, the algebra that results will be an analog of Boolean algebra, orin other words an algebra of logic.

In fact we can interpret this boxalgebra for logic as follows:

(a) A box stands for the valueTRUE. An empty space or a doubled box stands for the value FALSE.

(b) stands for NOT A.

(c) AB stands for A OR B.

We leave it as an exercise for you to see that

stands for A AND B and that

stands for A IMPLIES B.

With this dictionary one can learn to do logic using the box algebra. It has anumber of interesting features. If you want to explore this topic further take alook at the book "Laws of Form" by G. Spencer-Brown where a version of thisarithmetic and algebra first appeared.

A very similar algebra for logicwas invented by the late nineteenth and early twentieth century logician andphilosopher Charles Sanders Peirce.

This section is a dialoguebetween Lou, the author of this piece, and George, an hypothetical reader.

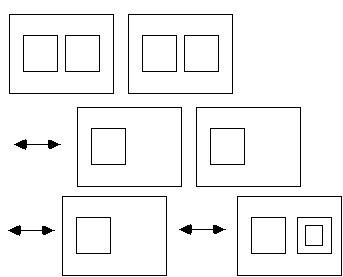
George. I have been working with your box algebra for a while now andI have some questions. My first question is this: You said that we can canceltwo empty boxes if they are adjacent to one another.

After awhile Irealized that you probably meant that

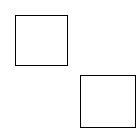
are adjacent and that we should be allowed to condense them to a single box. But I also would like to condense the two large empty boxes in the followingexpression. Are they adjacent?

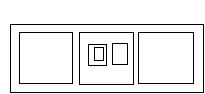
Lou. Those two boxes are not directly next to one another. I would notcall them adjacent if they were tables in a restaurant.

However it is truethat we can condense them and allow the move:

So we need a technical definition of "adjacent" thatwill work for our

purposes. We will say that two boxes are in the samespace if it is possible to draw a path from the outside of one to the outsideof the other that does not cross any boundaries in the expression. This path isnot necessarily a straight line. So in the situation we are discussing we see

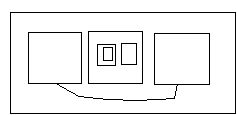
with the connection between these two boxes showing that they are in the samespace. Now we shall simply define two boxes to be adjacent if they are inthe same space and let it go at that. This notion of adjacency is not quite aslocal as the English use of the term, but it will work for our purposes.

George. Ok. I am satisfied with that, but I notice that another way wecould handle adjacency would be to only allow the boxes to occur in rows. Thus Iwould take an expression like

and rewrite it (without using rules expect my ability to rearrange the boxes)to the form below.

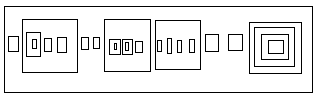
Then I can take adjacency to mean that one box is directly to the right or theleft of the other, and that neither box contains the other.

Lou. That is a good point! You are observing that as far as valuationof an expression is concerned, the only relationship we need to know about twoboxes is whether one box is inside the other or not. Thus we can rearrange theboxes so that they line up horizontally, and proceed to do cancellation andcondensation on them using direct adjacency. Notice that with respect to thisordering from left to right, you are assuming the commutative law. That is youare assuming that AB is the same as BA when AB denotes the result of juxtaposingtwo expressions in direct adjacency. In particular we have

This is of course perfectly compatible with our evaluations.

George. In fact, if we linearly order the expressions from left toright, then they are the same in structure as parentheses. I mean I can write [[] [[ ]] ] instead of the left expression in boxes above.

Lou. That is certainly true and it is a good way to abbreviate theseboxes and a good way to input these expressions into a computer. We can also usethe parentheses to translate box algebra into more traditional forms of algebra. I will come back to this point in later sections of the discussion.

George. But I would like to know how you will prove that there is noway to transform the empty box to an empty space.

Lou. Did you try to prove it?

George. No.

Lou. Well try to do it, and then we will talk about that.

George. I have been thinking aboutthat problem, and I am confused. It seems quite obvious to me that there is noway to transform a box to an empty space, but how do you prove it?

Lou. Well first of all, it helps to see that if we had defined thinksdifferently then the catastrophe could happen! Consider a parenthesis basedsystem with the rules

< > = << >> < > =<< > >< >

= << > > = << >> = .

So in this system it is possible forthe box (in parenthesis form) to disappear!

George. That was not fair! You divided the box into the left andright pieces and then let the pieces act separately!!

Lou. It is true. I did that. But it was an example of a formal systemin which creation/cancellation, expansion/condensation occur and nevertheless the"box" can disappear. This example shows that we should make a proof for our boxarithmetic.

George. All right. I will work on it.

Lou. Here is a hint. Think of a box expression as a signal processor.Suppose that there is a signal in each empty box, that every time the signal"goes out" into boxes of smaller depth they are inverted when they cross a boxboundary.

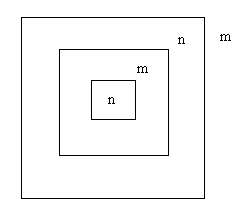
Here I have illustrated this idea using two signal values. One value is n (fornot marked). The other value is m (for marked). In the expression above, we givethe deepest space the value n and watch the signal bubble upward. It crosses oneboundary and becomes m. Then it crosses another boundary and becomes n, andfinally a third boundary and becomes m in the space of depth zero. Incidentally,I will call the space of depth zero the shallowest space.

George. I see! And the final value is in fact the value of theexpression consisting of the nest of three boxes. But what will you do with thisone I wonder?

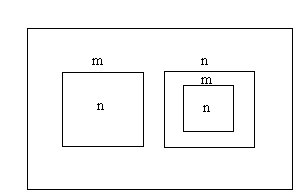
Here I have put unmarked signals in the deep empty spaces of the expression,and I have bubbled them up according to your rules as far as I could. But I endup with an m and an n in the same space at depth 1. What do I do now?

Lou. Well, if m means marked and n means unmarked, what would m next ton mean?

George. Oh! m next to n means marked next to unmarked but that wouldstill be marked. I see. We can use the following rules:

When it is marked thenit is marked. The only way to be unmarked is to be unmarked. Is this philosophy? Well look, I will continue to calculate:

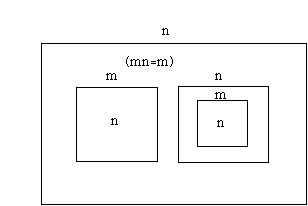
So the calculation says that this expression is unmarked, and indeed if Itransform it will go away!

Lou. Right. This is a method for calculating in a completely standardway a value of n or m for any expression. Now you can do the exercise to showthat if you change the expression according to one of our rules, this value doesnot change. And clearly the single empty box has value m while the empty spacehas value n. Since m and n are distinct, this proves our result.

George. How do you know that m and n are distinct?

Lou. Careful! You are crossing a boundary with that question.

It is given that m and n are distinct symbols that we are calculating with. Wesee that any calculation with m's and n's is just a string of them like mmnmnnn.And the value of such a string is m if there is an m in the string. The value ofthe string is n is there is no m in the string. The use of m and n depends uponour ability to distinguish at all. If we could not make two distinct symbols towork with, then there would be no hope of doing any mathematics at all. In thissense the possibility of doing mathematics is the same as the possibility thatthere is a distinction.

George. Well. Where do we go from here?

Lou. Algebra and onward! But lets take a rest right now.

George. Wait. I don't want to quitjust yet! I have another question.

Lou. Yes?

George. What about infinite expressions? I know that we cannot reducethem all to marked or unmarked states, but can't we study them anyway?

Lou. Certainly! Lets slow down a bit. Now the expression J that I amdrawing here is perhaps the simplest example of an infinite expression. It is aninfinitely descending nest of boxes.

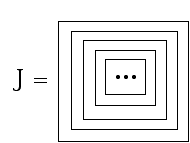
There is no way to evaluate J using our rules, since J has no deepest space,and hence no instance of condensation or cancellation. Notice that I cannotactually write J. What I write contains those famous three dots in a deepestspace. The three dots mean that you have to

go on in the same pattern"forever". This expression J is a mathematical idealization. It does not existas an entity that can be fully written out. However, J does have a very nicedescription in terms of itself. We can write J equal to a box around itself!

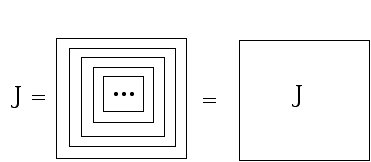
In other words, this infinite expression J is sitting inside itself.

We say that J reenters its own indicational space.

From thisreentering property you can see how J has no hope to be equal to either a markedstate or an unmarked state. For suppose that J is marked. Then J would be equalto a box around a box, but this is unmarked! And if J is unmarked, then theequation will tell us that J is marked.

We already knew that J could not be reduced to a marked state or to anunmarked state, but now we know that it would be inconsistent to assign it such avalue. If J is to be a value in logic, then it is a value that heads on outbeyond true and false. J is analogous to numbers like the square root of minusone, numbers that cannot be part of the real line. such numbers are calledcomplex or imaginary. Similarly, we shall call J an imaginary (logical)value!

George. I see what happened to you. You fell into thethinking that mathematicians always fall into. You think that the infinite nestof marks in J exists "all at once" in some timeless domain. And then you lookinside the mark around the outside of J and see that inifinity in the samepattern. And so you get your equation.

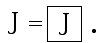
That is fine for idealists, but I am going to take a different view about whatyou just told me. I am going to to understand that an equals sign in the form A = B really means "replace A by B". That is the way I use it when I amprogramming a computer. The mind is just another computer. You think things canbe "equal". I deny it!

The equals sign just means that one "thing" can bereplaced by another thing and in either order, unless one decides upon an order.

Now lets see what your equation says. Suppose J = , then the equation says " replace a box by a box around abox" or "replace a box around a box by a box around that." I will emphasize thisby writing a double arrow instead of that equals sign.

But the equation does not say that you cannot do it again so I really shouldwrite as follows.

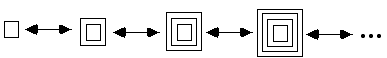
If you follow the process to the right, it starts building the infinite form.Now I know it never gets there, but is this not a much better and more concreteview of the situation? The clock ticks, and at each tick a new box is added tosurround the old nest of boxes.
At each tick of the clock the value of theexpression changes

from marked, to unmarked, to marked , to unmarked, andso on.

Your J is just an oscillator. It is no more paradoxical thana doorbell or a buzzer. Furthermore J is either marked or unmarked at any giventime! You got confused when confronted with temporality. You want to collapsethe passage of time into an eternal and everlasting geometry of the present.

Lou. There is certainly merit in what you say, but I do want to treatthe algebra in a way that does not depend upon time. If we take J to satisfy theequation and use the usual rules ofsubstitution and replacement in algebra, then it is easy to arrive at acontradiction. For example, lets suppose that J satisfies all the rules thatfinite expressions satisfy at the algebraic level. Then since

  for any P, we have .

But if and , then and thisis a contradiction. That is, if we attempt to include J in this standard way,then the whole system will collapse!

George. You are right, and I realize that one way to handle thissituation would be to give up some of the algebraic rules that hold for finiteexpressions. However, there is another way due to Jim Flagg. I am sure you knowit. In the Flagg Resolution we say that while 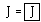, there is only one J and so if you change J to J with a box around itsomewhere, then you must make this change everywhere! With this principle inmind, you cannot make the step

.

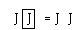The best you can do is

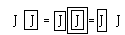
and this will hardly lead to any contradictions!

The Flagg resolution lets us keep the basic algebra and still include temporalexpressions like J. Saying that there is only one J and that substitutions mustbe performed everywhere is way to include the temporality in the algebra.

Lou. I like the Flagg Resolution. We should explore the world ofinfinite expressions using it.

George. Thanks. Lets do that.