Algebra, what are the difference between evaluation and simplification of an expression , algebra linear equations graphing worksheet , addition and subtraction of fractions worksheets lcd , solve quadratic equation for the specified variable , calculating a 3rd order polynomial with one variable , algebra square root solver , java code convert mixed fraction to decimal , solving solving binomial equations india , algebra square cube roots interactive lessons , partial differential equation solution first order linear , math equations percent algebra formulas , free answers for comparing linear combination methods for solving systems of equation in a chart , algebraic equation with fractional exponent , addition and subtraction formulas solved problems , simplifying radicals absolute value , sat prep formulas square root , free Algebra calculator for Rational Expression , java examples to find the number & sum of integers divisible by 7 , ti 83 plus factoring complex number , ti-89 convert number base 6 to number base 3 , Algebra expressions, what is the difference between evaluation and simplification of an expression? , charts and graph on the comparison of substitution and linear combination , online algebra calculator square root , simultaneous linear equation in two variable for class ten , substitution method is easier than the addition method when one of the equations is very simple and can readily be solved for one of the variables , quadratic formula square root method , cube root calculator TI-83 plus how to do , free solving equations with fractional coefficients help , how to solve a 2nd order differential equations , factorization fraction quadratic equations equation , square root revision for calculator common entrance , maple solve nonlinear multivariable two equations problems examples , multiplication division rational expressions problem solvers , Algebra help with factoring sums of cubes
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: why use factoring to solve quadratic equations. We have an extensive database of resources on why use factoring to solve quadratic equations. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!

---

Solving Quadratic Equations


Let's examine the example from the previous page:

In that example, we had an equation of the form:

t² - 10t - 600 = 0

which we factored into two terms as follows:

(t + 20) (t - 30)

The answer would be t = -20 and t = 30. Since -20 has no meaning, the answer is simply 30.

What if we cannot factor the equation?

Suppose that another project has a cost function of the form:

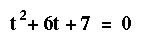
This equation cannot be factored as in the first example. One way to solve this particular equation is by completing the square. We first move the 7 to the right hand side of the equal sign.

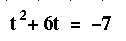
Then we proceed to add a number squared to both sides of the equation to complete the square as follow:

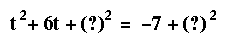
At this point, the number has to be guessed.

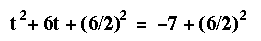
When we reduce the equation, we get

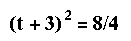
The equation yields two answers


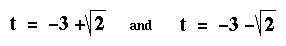
If we cannot factor the equation, we can still solve it by the method of completing the square as shown in the above example.



A few simple facts that you should know

---

Did you know that there are other methods for solving a quadratic equation, such as factoring, completing the square, or using the quadratic formula?



How do I know which method to use?

• Use factoring when the equation is simple and the factors are obvious. Use completing the square when you cannot factor the equation. When in doubt, use the Quadratic Formula, shown on the next page, which works for any quadratic equations.

What is actually meant by solving a quadratic equation?

• Solving a quadratic equation means finding the values of x where the graph cuts the x-axis.

Do you know how the graph for a quadratic equation look?
The graph for a quadratic equation is a parabola.

• If the parabola cuts the x-axis at only one point it means that the quadratic equation has two solutions with the same value (the value of x where the parabola touches the x-axis).
  
  
  
• If the parabola cuts the x-axis at two points it means that it has two solutions (the points where the parabola crosses the x-axis).
  
  
  
• If the parabola doesn't cut the x-axis it means that the quadratic equation doesn't have any real solution.
  

Try to find the solutions of x² + 1 , x² + 2x + 1 , x² - 1 by using the Graphing workbench .