Get it on Google Play Get it on Apple Store



ADDITION AND SUBTRACTION FORMULAS SOLVED PROBLEMS
free solving equations with fractional coefficients help, charts and graph on the comparison of substitution and linear combination ,   Algebra help with factoring sums of cubes ,   solve quadratic equation for the specified variable ,   maple solve nonlinear multivariable two equations problems examples,   square root revision for calculator common entrance , algebra square cube roots interactive lessons, Algebra, what are the difference between evaluation and simplification of an expression ,   free answers for comparing linear combination methods for solving systems of equation in a chart ,   how to solve a 2nd order differential equations ,   Algebra expressions, what is the difference between evaluation and simplification of an expression? ,   sat prep formulas square root ,   java examples to find the number & sum of integers divisible by 7,   free Algebra calculator for Rational Expression ,   simplifying radicals absolute value ,     java code convert mixed fraction to decimal , multiplication division rational expressions problem solvers ,   quadratic formula square root method,   ti 83 plus factoring complex number , ti-89 convert number base 6 to number base 3 ,   solving solving binomial equations india ,   substitution method is easier than the addition method when one of the equations is very simple and can readily be solved for one of the variables,   why use factoring to solve quadratic equations ,   algebra square root solver,   simultaneous linear equation in two variable for class ten,   algebraic equation with fractional exponent , cube root calculator TI-83 plus how to do , partial differential equation solution first order linear , online algebra calculator square root ,     algebra linear equations graphing worksheet , math equations percent algebra formulas ,   factorization fraction quadratic equations equation, addition and subtraction of fractions worksheets lcd, calculating a 3rd order polynomial with one variable  
   Thank you for visiting our site! You landed on this page because you entered a search term similar to this: addition and subtraction formulas solved problems, here's the result:

CHAPTER #2 - EQUATIONS, INEQUALITIES, AND PROBLEM SOLVING (pp. 44 to 104)

LESSON #2.1 - The General Objectives of this lesson is to study first-degree equations in one variable.

PERFORMANCE OBJECTIVES - At the end of this lesson the student will be able to:

  • Explain what is meant by equivalent equations.
  • Solve a first-degree equation in one variable by reducing it to an equivalent equation.
  • Solve word problems involving first-degree equations in one variable.

WORD PROBLEMS - Included in the lesson.

2.1 - Solving First-Degree Equations - To begin our discussion of solving first-degree equations in one variable we need the following definitions.

  1. An equation is a mathematical statement that expresses the relation of equality between two expressions.

    a)  15 - 2 = 13

    b)  3x + 6 = 12

    c)  x2 - 4 = (x+2)(x-2)

  2. A solution is any value of the variable that satisfies the equation. For example for the equation -

    3x + 6 = 12

    the value of x = 2 yields

    3*2 + 6 = 12.

    Since this value of x made the equation a true statement, it is a solution. It should be noted that this particular equation only has one solution.

  3. An identity is an equation that is true for all values of the variable. For example the equation -

    x2 - 4 = (x+2)(x-2)

    is true for all values of x.

  4. Equivalent equations are equations that have the same solution. For instance -

    a)  3x + 6 = 12

    b)  3x = 6

    c)  x = 2

    all have the same solution, x = 2, therefore they are equivalent equations.

  5. A first-degree equation in one variable is one where the highest exponent on the variable is one. Examples include:

    a)  3x + 6 = 12

    b)  x - 17 + 2(x+1) = 3(x-1) + 5x

    First degree equations are solved by reducing them to equivalent equations, where the solution is obvious. This is done by using the following two properties of numbers.

Addition/Subtraction Property of Equality - The addition (subtraction) of the same number to (from) both sides of an equation produces an equivalent equation. That is, if

P = Q

then   P + R = Q + R

or   P - R = Q - R.

Multiplication/Division Property of Equality - The multiplication (division) of both sides of an equation by the same number produces an equivalent equation. That is, if

P = Q

then   P*R = Q*R

or   P/R = Q/R.

 

Example - Solve the equation: x -

17 + 2(x+1) = 3(x-1) + 5x.

    Step 1 - Simplify both sides of the equation as much as possible.

    x - 17 + 2x +2 = 3x -3 + 5x 3x -15 = 8x -3

    Step 2 - Use the addition property to isolate the variable on one side of the equation.

    3x - 15 - 3x + 3 = 8x - 3x - 3 + 3

    -12 = 5x

    Step 3 - Use the multiplication property to reduce the coefficient of the variable to one.

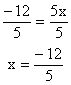
    Step 4 - Substitute the answer in the original equation to make sure it works.

 

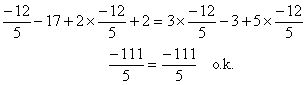
Use of Equations to Solve Problems - As you can see from the previous two examples, solving first-degree equations in one variable is not too difficult. On the other hand, solving word problems, which give rise to first-degree equations, often causes us much anxiety and grief. The difficulty occurs in translating the problem expressed in standard language into mathematical terms. Fortunately, for all of us, there are some rules that can be followed which can help us to overcome this difficulty.

Rules for Solving Word Problems -

    Step 1. Read the problem very carefully, making sure you understand what is stated and what is being asked for.

    Step 2. If a diagram is appropriate, sketch it, and use it to solve the problem.

    Step 3. Answer the following question.

    What am I looking for?

                Write down the answer, and then give the quantity(s) a mathematical name(s) such as x, y, etc.

    Step 4. Write down any other quantities specified in the problem along with appropriate mathematical names. Use a table as an organizing tool when appropriate.

    Step 5. Rewrite the problem in the form of an equation, focusing on keywords such as plus, is, equal to, difference of, etc.. (Refer to page 34 in the text.)

    Step 6. Solve the equation for the unknown variable.

    Step 7. Check the solution to see if it agrees with the facts in the problem. As an aid, answer the following question if you can.

    Does the solution make sense?

    If the answer to this question is yes, the odds are very good that you solved the problem correctly. If the answer is no, go back and resolve the problem.

Board and Class Problem - Page 51/ 59, 65.

 

LESSON #2.2 - The General Objective of this lesson is to develop a procedure for solving fractional equations.

PERFORMANCE OBJECTIVES - At the end of this lesson the student will be able to: Identify a fractional equation. Solve fractional first-degree equations in one variable.

2.2 - Equations Involving Fractional Forms - Any equation containing one or more fractions can be classified as a fractional equation. Usually the first step to be carried out is to multiply both sides of the equation by the least common denominator (LCD).

Least Common Denominator - To find the LCD you follow the following procedure.

    Step 1. Factor each denominator into a product of its prime factors.

    Step 2. List each prime factor with the largest exponent it has in any factored denominator.

    Step 3. The LCD is the product of the factors listed in Step 2.

     

Board and Class Problem - Find the sum of

    Step 1. Discuss how to find prime factors.

    324 = 22 * 34      and       144 = 24 * 32

    Step 2. The factors for the LCD are 2 and 3.

    Step 3. The LCD = 24 * 34.

    Solve the problem on the board. (The answer is 13/1296.)

Procedure for Solving Fractional Equations -

    Step 1. Determine the LCD for the fractions in the equation.

    Step 2. Multiply both sides of the equation by the LCD.

    Step 3. Solve the resulting equation for the unknown.

    Step 4. Substitute the solution from Step 3 into all of the denominators to ensure that no denominator equals zero. If any denominator equals zero, reject the 'apparent solution.'

Board and Class Problems - Pages 58 to 59/22, 29, 49.

 

LESSON #2.3 - The General Objective of this lesson is to deal with equations involving decimal coefficients.

PERFORMANCE OBJECTIVES - At the end of this lesson the student will be able: Solve discount problems. Solve sales problems. Solve simple interest problems.

2.3 - Equations Involving Decimals and Problem Solving - Any equation containing decimal coefficients can be solved as previously described, however, it is often convenient to clear the equation of all decimals by multiplying by an appropriate power of ten. This often occurs with discount, sales, and investment problems.

Discount Problems - Let

P = original price
S = sales price
D = discount
then

S = P - D

Sales Problems - Let

P = profit
S = sales price
C = cost
then
S = C + P

Investment Problems - Let

P = principal invested for one year
r = interest rate
I= interest earned for one year
t = time period
then
I = rP

Board and Class Problems - Pages 65 to 66/29, 41.

 

LESSON #2.4 - The General Objective of this lesson is to deal with literal equations or formulas.

PERFORMANCE OBJECTIVES - At the end of this lesson the student will be able to manipulate formulas, solving for each variable in terms of the others.

2.4 - Formulas - Formulas are rules that are stated in symbolic form, usually as equations. As we saw in the word problem involving temperatures, formulas can be solved for a specific variable if we are given numerical values for the other variables. We can also manipulate the formula enabling us to solve for any variable in terms of the other, using our rules for solving equations.

Board and Class Problem - The following formula is used by electrical engineers in studying simple parallel circuits.

where R1, R2 and R3 are three parallel resistance's in the circuit, and R is the total resistance of the circuit. Solve for R in terms of the other three resistance's. Write down each step in the solution.

Formulas and Problem Solving - Solving word problems is simplified by developing common techniques that can be used to solve any problem. It also depends upon knowing the formula that applies to the particular problem being investigated. We will consider some different types now.

 

Simple Interest - The equation for simple interest for t years is given by -

A = P + Prt

where

    A = amount accumulated after t years
    P = principal
    r = interest rate
    t = time

Board and Class Problem - Page 76/49.

Uniform Motion - The equation for uniform motion is given by -

d = vt

where

    d = distance traveled
    v = speed
    t = time

Word problems of uniform motion usually involve two different motions. The following table helps organize such problems and is a useful aid for developing the appropriate equation.

Trip Distance Speed Time
Motion 1 d1 v1 t1
Motion 2 d2 v2 t2