|
|
 |
|
|
 |
|
 |
| |
SOLVING SOLVING BINOMIAL EQUATIONS INDIA
algebra square cube roots interactive lessons,
math equations percent algebra formulas,
sat prep formulas square root ,
factorization fraction quadratic equations equation ,
partial differential equation solution first order linear ,
calculating a 3rd order polynomial with one variable ,
Algebra expressions, what is the difference between evaluation and simplification of an expression? ,
Algebra help with factoring sums of cubes ,
why use factoring to solve quadratic equations ,
Algebra, what are the difference between evaluation and simplification of an expression,
substitution method is easier than the addition method when one of the equations is very simple and can readily be solved for one of the variables ,
free solving equations with fractional coefficients help,
cube root calculator TI-83 plus how to do,
online algebra calculator square root,
simultaneous linear equation in two variable for class ten ,
ti-89 convert number base 6 to number base 3 ,
simplifying radicals absolute value ,
algebraic equation with fractional exponent ,
ti 83 plus factoring complex number,
algebra linear equations graphing worksheet ,
addition and subtraction of fractions worksheets lcd,
java examples to find the number & sum of integers divisible by 7 ,
multiplication division rational expressions problem solvers,
java code convert mixed fraction to decimal ,
algebra square root solver,
free answers for comparing linear combination methods for solving systems of equation in a chart ,
square root revision for calculator common entrance ,
charts and graph on the comparison of substitution and linear combination ,
how to solve a 2nd order differential equations ,
quadratic formula square root method ,
solve quadratic equation for the specified variable,
maple solve nonlinear multivariable two equations problems examples ,
free Algebra calculator for Rational Expression ,
addition and subtraction formulas solved problems
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving solving binomial equations india, here's the result:
Europeans Prior To Pascal
Who Knew About The Triangle
|
Blaise Pascal
was not the first man in Europe to study the binomial coefficients, and
never claimed to be such; indeed, both Blaise Pascal and his father
Etienne had been in correspondence with Father Marin Mersenne, who
published a book with a table of binomial coefficients in 1636.
Many authors discussed the ideas with respect to expansions of
binomials, answers to combinatorial problems and figurate numbers,
numbers relating to figures such as triangles, squares, tetrahedra and
pyramids.
Here is a
short list in chronolgical order of publishing.
Ancient Greek Era
Until recently, little
had been known of the Greeks interest in combinatorics; it was known
that they studied square numbers and triangular numbers, the second
column of the Triangle,  , so they knew that the sum of two
consecutive triangular numbers forms a square, which is in our
identity database as #1200002.
Recently a lost manuscript of
Archimedes was rediscovered in a palimpsest, a text written over
another older text. Archimedes' work was bleached out and the
parchment was cut to make paper for a prayerbook about 1000 years
ago. Using modern techniques, the work Archimedes did was
restored, and it was shown he had correctly figured out the number of
different ways a geometric puzzle called the Stomachion
could be reassembled into a square; while Archimedes does not use the
binomial coefficients, it does show an interest in counting previously
unseen in surving texts from the classical Greek period.
The First Millenium (from 0 to 1000 A.D.)
Circa 100 A.D.: Two authors, Theon of Smyrna and Nicomachus
of Gerasa, saw that the sum of triangles could be seen as a
tetrahedron, so the tetrahedral numbers, the third column of the
Triangle,  , were first seen in the West. To generalize this
concept for figures, the mathematicians of the day would have to
think beyond three dimensions. It would be over a millenium
before another European would extend this work.
275: Porphyry correctly lists the number of pairs of five
voices is not 5×4=20, but 5×4/2=10.
His work is a commentary on Aristotle's Categories.
320: Pappus of Alexandra generalizes Porphyry's work.
Circa 510: Boethius, writing a commentary on Porphyry's
work, repeats the generalization found by Pappus.
10th Century A.D.: Sortes Apostolorum published,
a book of fortune telling by dice rolls. Similar publications,
including 1484's Libro della Ventura are the impetus for
Tartaglia solving the general problem of how many different dice
rolls there are given k dice, each with n sides.
The Second Millenium (from 1000 A.D. until Pascal)
1140: In Spain, Rabbi Ben Ezra figures out the seventh
row of the Triangle, in connection with the question of how to take the
Sun and the six known planets (Mercury, Venus, Earth, Mars, Jupiter
and Saturn) in combinations of one at a time, two at a time, etc.
1202: Fibonacci (also known as Leonardo of Pisa) writes
down the expansion of (a+b)3, which was already
well-known in India and the Middle East. Besides being know for
the Fibonacci numbers, he is also credited with being the first
European mathematician to use the Hindu-Arabic numerals we use today,
which made the Roman numeral system obsolete.
Circa 1225: Jordanus of Nemore, a German mathematician,
in his manuscript de Arithmetica shows that he understands both 
, the second of which is remarkable step forward for the mathematics
of his day. Jordanus dies young, lost at sea on the return trip
from The Holy Land.
13th Century, exact date unknown: In a poem entitled de
Vetula, it is shown that three six-sided dice can come up in 56
different ways, if we count 6-6-5 to be the same as 6-5-6 and 5-6-6, for
example.
1321: Levi Ben Gerson, a Frenchman came up with the
falling factorial formula for the binomial coefficients, and presents
the first known examples of an explicit mathematical induction proof.
Both Ben Gerson and Ben Ezra were interested in the Hebrew
mystical tradition of the Cabala, which has an interest in, among other
things, seemingly magical relationships between numbers.
Circa 1407: an edition of Jordanus' de
Arithmetica contains the following table.
|
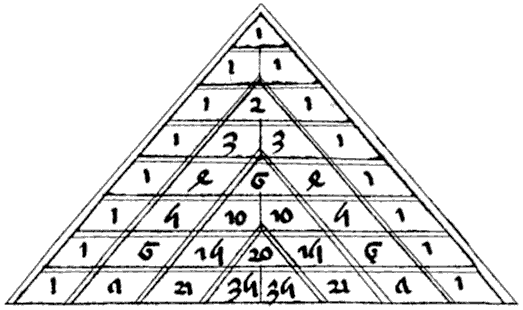Note the somewhat strange obsolete versions
of the numerals 4, 5, 6 and 7, while 0, 1, 2 and 3 are easily
recognizable in their modern form.
|
1484: Lorenzo Spirto's Libro della Ventura (Book of Fortune)
lists the 56 ways 3 six-sided dice can be thrown in nearly exactly the
same way described in the poem de Vetula from two centuries
before. This is the inspiration for Tartaglia to solve the
general problem for k dice, each with n sides in 1523,
which is  .
1523: Nicolo Tartaglia first publishes the generalization
of the figurate numbers. Some 30 years later, in his General
Treatise, he publishes the Triangle in table form.
Tartaglia is the first mathematician to publish a general
formula for solving cubic equations. His name in Italian means
"stammerer". This cruel nickname was given to him after severe
facial wounds he suffered at the age of twelve when attacked by a
soldier invading his hometown of Brescia nearly killed him; these wounds
left him able to speak only with difficulty for the rest of his life.
1539: Gerolamo Cardano, the Italian algebraist, correctly
determines that the number of ways to take 2 or more things from a set
of n things is 2n-n-1, which is the sum of
the nth row of the Triangle if we ignore the first
two entries.
1544: The German mathematician Michael Stifel publishes
the extended Figurate Triangle in the figure shown below. Stifel
gives credit to Cardano's work published five years earlier.
|
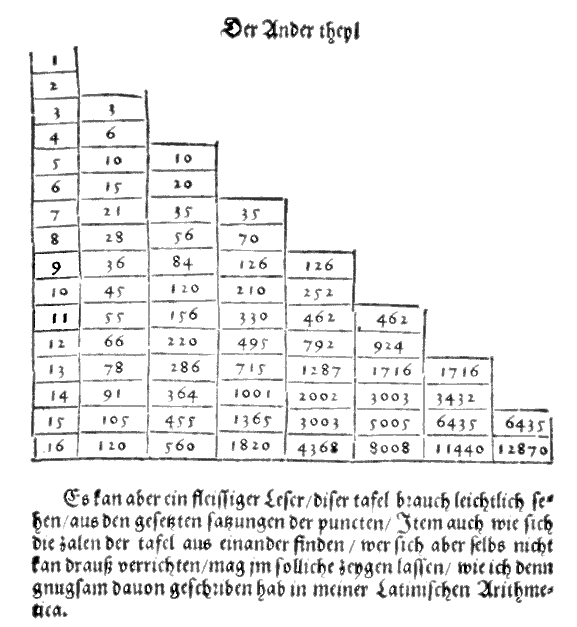To turn this into Pascal's Triangle,
we would need to add a column of 1's at the beginning, and then mirror
the numbers listed on the left onto the right side, except for the
rightmost entry in the even rows and the two rightmost entries in the
odd rows.
|
1545: Scheubelius, another German, publishes his version of the
Triangle in connection with the extraction of roots, the great unsolved
problem of the age in its most general form.
|
Not as neat as Stifel's work a year earlier,
and with the obvious errors of "41" and "51" at the end of rows 14 and
15 (there's also a "0" in row 10 that should be 120), Scheubelius'
work does show that the Triangle is symmetric, which isn't clear in
Stifel's representation.
|
1556: Tartaglia publishes his General Treatise,
which includes the following tables of the Triangle
 |
The first page of Tartaglia's General
Treatise, with the Triangle written in rectangular form
|
|
Also from Tartaglia, the Triangle in
symmetric form, with the 1's removed from both left and right
|
1570: Cardano publishes his Opus Novum (New Work), which
includes the following page.
|
Cardano's 1570 work, which states the
figurate numbers are the combinatorial numbers
|
1591: François Viète gives
names to the first few columns of the Triangle in Latin; "numeri
trianguli", "pyramidales", "triangulo-trianguli", "triangulo-pyramidales"
These names are also used in the next century by Pierre de Fermat,
who was Pascal's main correspondent in solving the Problem of
Points, and William Oughtred, a British mathematician who influences
many of his countrymen who come after him.
1631: William Oughtred publishes his Clavis Mathematicae,
which influences his student John Wallis and is later owned in a 3rd
edition printing ; both Wallis and Newton are
instrumental in the work that connects the binomial coefficients to the
new field of calculus later in this century.
1633: The lifetime work of Henry Briggs
entitled Trigonometria Britannica is published two years after
his death by his friend Henry Gellibrand; he has a chapter on the
figurate numbers, which he refers to as "the calcuator of many uses".
1636: Father Marin Mersenne publishes his Harmonicorum
Libri XII; Mersenne in his life meets with both Blaise Pascal and
his father Etienne, and there is little doubt both of them read the
book and saw this table.
|
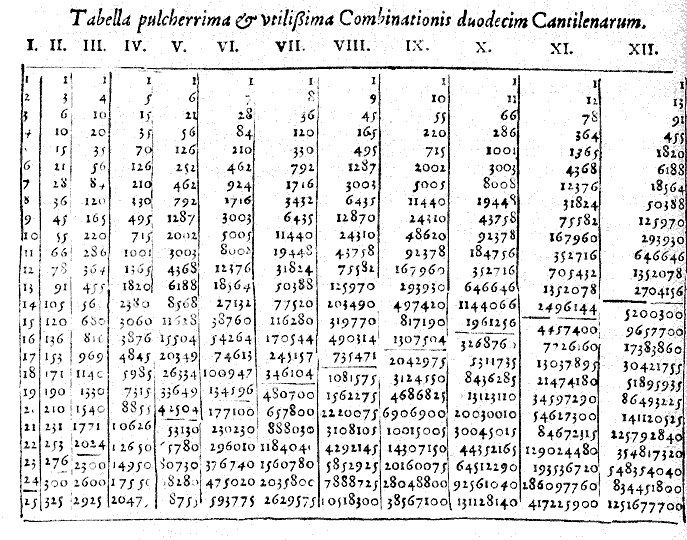While missing the first row of 1's, this
table does correctly show that "36 choose 12", the number in the lowest
right hand position, is over 1.2 trillion, a remarkable feat of
patience for a person calculating all these numbers by hand.
|
|
|
 |
|
 |
|
|
