Intermediate Algebra
Tutorial 9:
Formulas and Problem
Solving
 Learning Objectives
|
After completing this tutorial, you should be able to:
-
Solve a formula for a given variable.
-
Use Polya's four step process to solve word problems involving formulas.
|
Introduction
|
| In this tutorial we will be solving problems using
formulas to help
us. In Tutorial 8: An Introduction to Problem Solving, we
had
to create our own equations based on the given information. However,
all
of the problems we will be solving in this tutorial will involve using
a formula to get to our final answer. We will be looking at such
formulas as compound interest, distance/rate, volume of a sphere, and
so
on. Since we are still problem solving, I will use Polya’s
four steps to Problem Solving as introduced in Tutorial 8: An
Introduction
to Problem Solving to step us through the word problems in this
tutorial. After going through this tutorial, you will be an old pro at
solving word problems involving formulas. |
| A formula is an equation that involves two or more
variables that have
a specific relationship with each other. |
Solving a Formula
for a Specified Variable
|
Basically, you want to get the variable you are
solving for alone
on one side and everything else on the other side (including variables
you are not solving for) using INVERSE operations.
Even though there is more than one variable in a
formula, you solve
for a specific variable using the
exact
same steps that you do with an equation in one variable, as shown in
Tutorial
7: Linear Equations in One Variable.
It is really easy to get overwhelmed when there is more
than one variable
involved. Sometimes your head feels like it is spinning when you
see all of those variables. Isn’t math suppose to be about
numbers?
Well, just remember that a variable
represents
a number, so if you need to move it to the other side of the equation
you
use inverse operations, just like you would do with a number.
|
 Example
1: Solve the equation P
= 2L + 2W
for L. |
Do you recognize this formula?
This happens to be the formula for the perimeter of a rectangle, where
P
= perimeter, L = length, and W
= width.
In this problem, we need to solve for L.
This means we need to get L on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for L:
|
 |
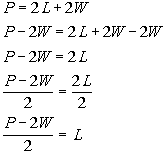*Inverse of add 2W
is sub. 2W
*Inverse of mult. by 2 is div.
by 2
*Formula solved for L
|
Example
2: Solve the equation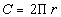 
for r. |
Do you recognize this formula?
This happens to be the formula for the circumference of a circle, where
C
=
circumference,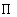 
= pi, and r = radius.
In this problem, we need to solve for r.
This means we need to get r on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for r:
|
 |
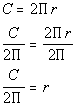*Inverse of mult. by 2pi is
div. by 2pi
*Formula solved for r
|
| Example
3: Solve the equation 5x
+ 4y = 11 for y. |
| This is an equation for a line. In later
tutorials, we will go
over graphing lines on a two dimensional graph. This is a little sneek
peak at working with a linear equation in two variables. When
graphing
such an equation, a lot of times, we have it written in what is called
the slope-intercept form, which boils down to solving the equation for
y. Lo and behold, that is what we are doing here (sneaky
how
we are slipping it in now, huh?). So if you get this concept down
now, you will be an old pro at it by the time we reach graphs.
In this problem, we need to solve for y.
This means we need to get y on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for y:
|
 |
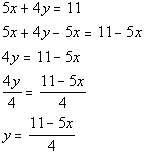*Inverse of add 5x
is sub. 5x
*Inverse of mult. by 4 is div.
by 4
*Formula solved for y
|
| Example
4: Solve the equation V
= lwh for h. |
Do you recognize this formula?
This happens to be the formula for the volume of a rectangular solid,
where V = volume, l =
length, w = width, and h
= height.
In this problem, we need to solve for h.
This means we need to get h on one side
and
EVERYTHING ELSE on the other side using inverse operations.
Let’s solve this formula for h:
|
 |
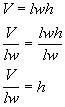*Inverse of mult. by lw
is div. by lw
*Formula solved for h
|
Polya’s Four-step
Process
for Problem Solving
(revisited)
|
As mentioned above, since we are still problem solving,
we will use
the exact same four step process we used in Tutorial
8: Introduction to Problem Solving. To refresh your
memory,
here they are again:
Step 1:
Compound interest is a type of word problem that
involves something
that we all can relate to - MONEY, MONEY, MONEY!!!
|
| Example
5: You recently received a windfall of $7000,
and
being the smart responsible person that you are, you invested it in an
account paying an annual percentage rate of 8%. Find the amount
in
the account after 9 years if the account is compounded quarterly. |
| Step 1: Understand
the problem. |
| Make sure that you read the question carefully several
times.
Since we are looking for compound interest, we will need
the compound
interest formula:
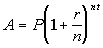
The variables in this formula represent the following:
A = ending amount in the
account
P = principal (starting
amount)
r = annual rate of interest
t = time in years
n = number of times
compounded per year
|
| Step 2: Devise
a plan (translate). |
In this problem,
A = ? = this is the variable we are looking for
P = 7000
r = 8% = .08
t = 9
n = 4 (There are
4 quarters
in a year)
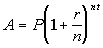
Plugging the values into the formula we get:
|
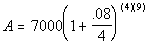
| Step 3: Carry
out the plan (solve). |
 |
*.08/4 = .02 and 4(9) = 36
*Add inside the ( )
*Raise 1.02 to the exponent of 36
*Multiply
|
| Step 4: Look
back (check and
interpret). |
If you take $7000 and compound it quarterly for 9
years, you do end
up with 14279.211.
FINAL ANSWER:
The compound amount is $14279.21.
|
| Example
6: It takes you 4.5 hours to drive from your
home
to your favorite weekend get away, which is 315 miles away. What
is your average speed? |
| Step 1: Understand
the problem. |
| Make sure that you read the question carefully several
times.
Since we are looking for speed, we can use the
distance/rate formula:
d =
rt
The variables in this formula represent the following:
d = distance
r = rate
t = time
|
| Step 2: Devise
a plan (translate). |
In this problem,
d = 315
r = ? = this is the variable
we are looking
for
t = 4.5
d =
rt
Plugging the values into the formula we get:
|
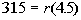
| Step 3: Carry
out the plan (solve). |
 |
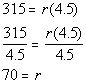*Inverse of mult. by 4.5 is
div. by 4.5
|
| Step 4: Look
back (check and
interpret). |
If you go at a rate of 70 miles per hour for 4.5 hours,
you would travel
315 miles.
FINAL ANSWER:
The average speed is 70 mph.
|
| Example
7: The diameter of a beach ball was found to be
18 inches. What is the volume of this beach ball? |
| Step 1: Understand
the problem. |
| Make sure that you read the question carefully several
times.
Since we are looking for the volume of a sphere,
we can use this
formula:
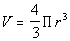
The variables in this formula represent the following:
V = volume of a sphere
r = radius
|
| Step 2: Devise
a plan (translate). |
In this problem,
V = ? = this is the variable
we are looking
for
r = 9 (radius is
half the diameter,
so r = 18/2 = 9)
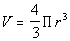
Plugging the values into the formula we get:
|
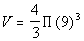
| Step 3: Carry
out the plan (solve). |
 |
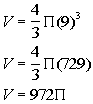*Cube 9
*Multiply
|
| Step 4: Look
back (check and
interpret). |
If you put in 9 for the radius, it does compute to have
a volume of  .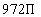
FINAL ANSWER:
The volume of the beach ball is 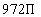cubic
inches.
|
| Example
8: One bag of fertilizer will cover 500 square
feet
of lawn. Your rectangular lawn is 70 feet by 50 feet. How
many
bags of fertilizer will you need to cover it? |
| Step 1: Understand
the problem. |
| Make sure that you read the question carefully several
times.
Since we are needing to find the area of a
rectangle, we can use
this formula:
A = LW
The variables in this formula represent the following:
A = Area of a rectangle
L = length
W = width
|
| Step 2: Devise
a plan (translate). |
In this problem,
A = ? = this is the variable
we are looking
for
L = 70
W = 50
A = LW
Plugging the values into the formula we get:
|
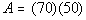
| Step 3: Carry
out the plan (solve). |
| First, find the area of the lawn: |
 |
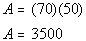*Multiply |
| For every 500 square feet, you need 1 bag of
fertilizer. So,
we need to see how many times 500 sq. feet goes into 3500 sq. feet to
find
the number of bags of fertilizer needed. |
 |
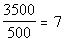*Divide |
| Step 4: Look
back (check and
interpret). |
If you take 70 times 50 you do get 3500, so the area
checks out.
And if you take 3500 and divide it by 500 you do get 7, so the number
of
bags needed checks out.
FINAL ANSWER:
7 bags of fertilizer.
|
Practice Problems
|
| These are practice problems to help bring you to the
next level.
It will allow you to check and see if you have an understanding of
these
types of problems. Math works just like
anything
else, if you want to get good at it, then you need to practice
it.
Even the best athletes and musicians had help along the way and lots of
practice, practice, practice, to get good at their sport or instrument.
In fact there is no such thing as too much practice.
To get the most out of these, you should work the
problem out on
your own and then check your answer by clicking on the link for the
answer/discussion
for that problem. At the link you will find the answer
as well as any steps that went into finding that answer.
|
 Practice
Problems 1a - 1b:
Solve each equation for the specified
variable.
|
1a. I = PRT;
for T
(answer/discussion
to 1a) |
1b. 3x - 7y
= 2; for y
(answer/discussion
to 1b) |
|
Practice
Problems 2a - 2c:
Solve the following word problems.
|
2a. A principle of $50,000 is invested into a CD
paying an annual
percentage rate of 7.5%. Find the amount in the account after 10
years if the account is compounded monthly.
(answer/discussion
to 2a) |
2b. In Nebraska on I-80, the speed limit is 75
mph. How
long would it take you to travel 525 miles in Nebraska on I-80 if
you went the speed limit the whole time?
(answer/discussion
to 2b) |
2c. Sally is training for the Olympics. She likes
to run around
a circular track that has a diameter of 60 yards, 20 times during a
workout.
How many yards does she run during her workout?
(answer/discussion
to 2c) |
Need Extra Help on These Topics?
|
The following are webpages
that can assist
you in the topics that were covered on this page:
This webpage helps you with solving formulas for a specified variable.
This webpage involves a
combination of problem
solving ideas from both Tutorial 8:
An Introduction to Problem Solving and Tutorial 9: Formulas and
Problem
Solving. It includes
problem
solving using formulas.
|
for
some
more suggestions.
|
All contents
June 22, 2003 |
