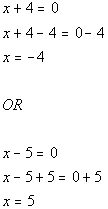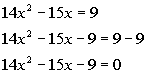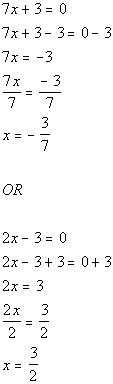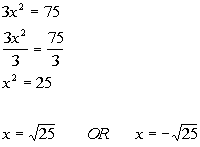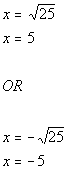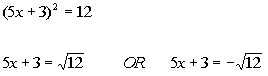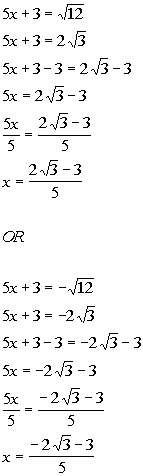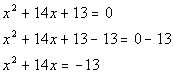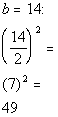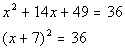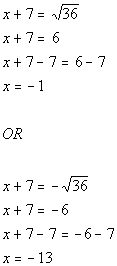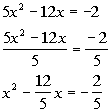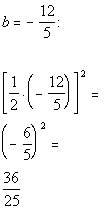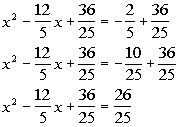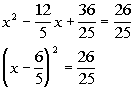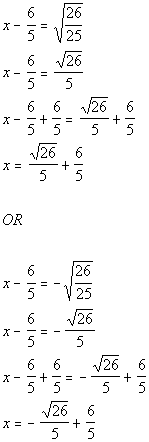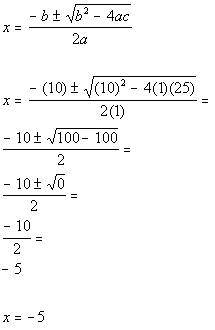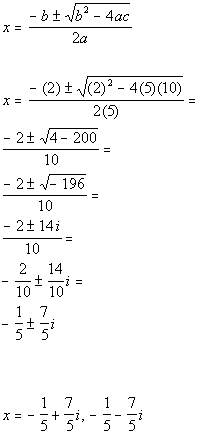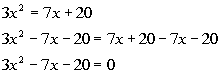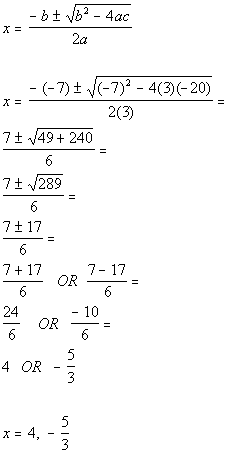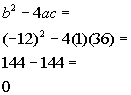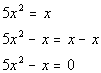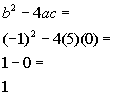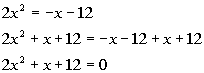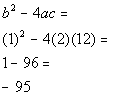quadratic formula square root method

QUADRATIC FORMULA SQUARE ROOT METHOD

charts and graph on the comparison of substitution and linear combination , solve quadratic equation for the specified variable , Algebra help with factoring sums of cubes , algebraic equation with fractional exponent , free Algebra calculator for Rational Expression , math equations percent algebra formulas , why use factoring to solve quadratic equations , partial differential equation solution first order linear , solving solving binomial equations india , algebra square cube roots interactive lessons , java code convert mixed fraction to decimal , substitution method is easier than the addition method when one of the equations is very simple and can readily be solved for one of the variables , multiplication division rational expressions problem solvers , calculating a 3rd order polynomial with one variable , how to solve a 2nd order differential equations , simultaneous linear equation in two variable for class ten , simplifying radicals absolute value , Algebra, what are the difference between evaluation and simplification of an expression , ti-89 convert number base 6 to number base 3 , addition and subtraction formulas solved problems , free answers for comparing linear combination methods for solving systems of equation in a chart , square root revision for calculator common entrance , online algebra calculator square root , maple solve nonlinear multivariable two equations problems examples , free solving equations with fractional coefficients help , java examples to find the number & sum of integers divisible by 7 , addition and subtraction of fractions worksheets lcd , ti 83 plus factoring complex number , cube root calculator TI-83 plus how to do , factorization fraction quadratic equations equation , Algebra expressions, what is the difference between evaluation and simplification of an expression? , sat prep formulas square root , algebra square root solver , algebra linear equations graphing worksheet
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: quadratic formula square root method. We have an extensive database of resources on quadratic formula square root method. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!

College Algebra
Answer/Discussion to Practice Problems
on Quadratic Equations

Answer/Discussion to 1a

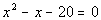
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form, 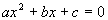, if needed.

This quadratic equation is already in standard form.

Step 3: Factor.

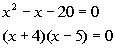*Quad. eq. in standard form
*Factor the trinomial

Step 4: Use the Zero-Product Principle

AND

Step 5: Solve for the linear equation(s) set up in step 4.

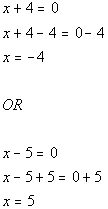*Use Zero-Product Principle
*Solve the first linear equation

*Solve the second linear equation

There are two solutions to this quadratic equation: x = -4 and x = 5.

Answer/Discussion to 1b

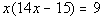
Step 1: Simplify each side if needed.

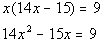*Use Dist. Prop. to clear the ( )

Step 2: Write in standard form, 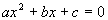, if needed.

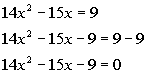*Inverse of add. 9 is sub. 9
*Quad. eq. in standard form

Step 3: Factor.

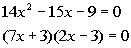*Quad. eq. in standard form
*Factor the trinomial

Step 4: Use the Zero-Product Principle

AND

Step 5: Solve for the linear equation(s) set up in step 4.

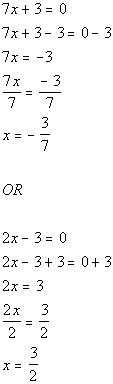*Use Zero-Product Principle
*Solve the first linear equation

*Solve the second linear equation

There are two solutions to this quadratic equation: x = -3/7 and x = 3/2.

Answer/Discussion to 2a

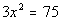
Step 1: Write the quadratic equation in the form if needed

AND

Step 2: Apply the square root method.

Note how this quadratic equation is not in th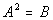e form

to begin with. The 3 is NOT part of the expression being squared on the left side of the equation. We can easily write it in the form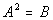

by dividing both sides by 3.

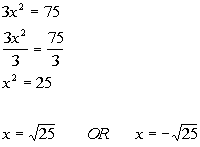*Not in the form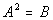

*Inv. of mult. by 3 is div. by 3

*Written in the form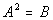

*Apply the sq. root method
*There are 2 solutions

Step 3: Solve for the linear equation(s) set up in step 2.

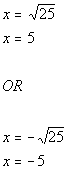*Sq. root of 25 = 5

*Neg. sq. root of 25 = -5

There are two solutions to this quadratic equation: x = 5 and x = -5.

Answer/Discussion to 2b

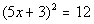
Step 1: Write the quadratic equation in the form if needed

AND

Step 2: Apply the square root method.

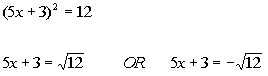*Written in the form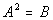

*Apply the sq. root method
*There are 2 solutions

Step 3: Solve for the linear equation(s) set up in step 2.

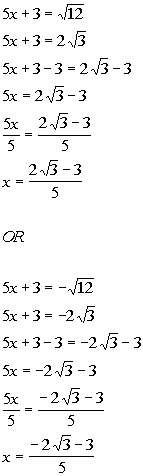*Sq. root of 12 = 2 sq. root of 3
*Solve for x

*Neg. sq. root of 12 = -2 sq. root of 3
*Solve for x

There are two solutions to this quadratic equation: x = 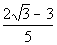and x = .

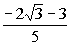Answer/Discussion to 3a

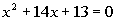
Step 1: Make sure that the coefficient on the term is equal to 1.

The coefficient of the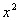

term is already 1.

Step 2: Isolate the 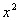and x terms.

Note how the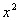

and x terms are not isolated to begin with. We can easily fix that by moving the constant to the other side of the equation.

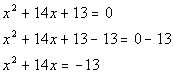*Inverse of add. 13 is sub. 13

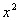* and x terms are now isolated

Step 3: Complete the square.

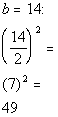*b is the coefficient of the x term

*Complete the square by taking 1/2 of b and squaring it

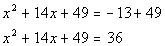*Add constant found above to BOTH sides of the eq.

*This creates a PST on the left side of eq.

Step 4: Factor the perfect square trinomial (created in step 3) as a binomial squared.

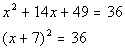*Factor the PST

Step 5: Solve the equation in step 4 by using the square root method.

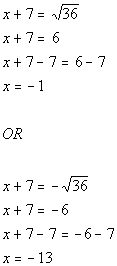*Written in the form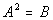

*Apply the sq. root method
*There are 2 solutions

There are two solutions to this quadratic equation: x = -1 and x = -13.

Answer/Discussion to 3b

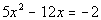
Step 1: Make sure that the coefficient on the term is equal to 1.

Note how the coefficient on the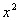

term is not 1 to begin with. We can easily fix that by dividing both sides by that coefficient, which in this case is 5 .

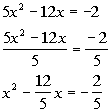*Divide both sides by 5

*Coefficient of 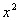term is now 1

Step 2: Isolate the 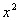and x terms.

The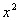

and x terms are already isolated.

Step 3: Complete the square.

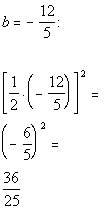*b is the coefficient of the x term

*Complete the square by taking 1/2 of b and squaring it

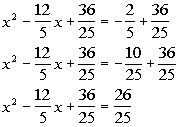*Add constant found above to BOTH sides of the eq.

*This creates a PST on the left side of eq.

Step 4: Factor the perfect square trinomial (created in step 3) as a binomial squared.

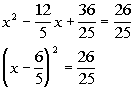*Factor the PST

Step 5: Solve the equation in step 4 by using the square root method.

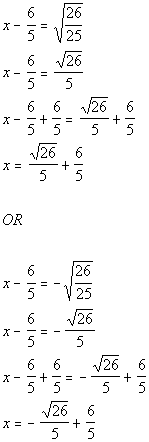*Written in the form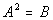

*Apply the sq. root method
*There are 2 solutions

There are two solutions to this quadratic equation: x = 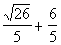and x = .

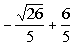Answer/Discussion to 4a

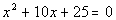
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form, 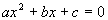, if needed.

This quadratic equation is already in standard form.

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 1.

b, the number in front of x, is 10.

c, the constant, is 25.

Make sure that you keep the sign that is in front of each of these numbers.

Next we will plug it into the quadratic formula. Note that we are only plugging in numbers, we don't also plug in the variable.

Step 4: Plug the values found in step 3 into the quadratic formula

AND

Step 5: Simplify if possible.

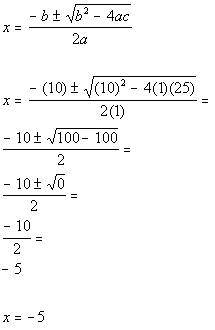*Quadratic formula

*Plug in values found above for a, b, and c

*Simplify

Answer/Discussion to 4b

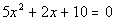
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form 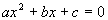if needed.

This quadratic equation is already in standard form.

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 5.

b, the number in front of x, is 2.

c, the constant, is 10.

Make sure that you keep the sign that is in front of each of these numbers.

Next we will plug it into the quadratic formula. Note that we are only plugging in numbers, we don't also plug in the variable.

Step 4: Plug the values found in step 3 into the quadratic formula

AND

Step 5: Simplify if possible.

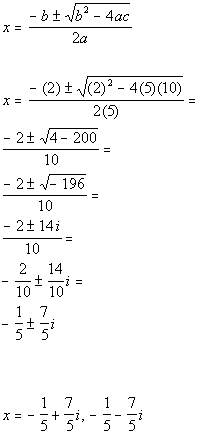*Quadratic formula

*Plug in values found above for a, b, and c

*Simplify

*Square root of a negative 1 is i

Answer/Discussion to 4c

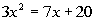
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form 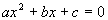if needed.

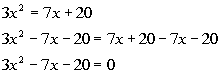*Inverse of add. 7x and 20 is sub. 7x and 20

*Quad. eq. in standard form

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 3.

b, the number in front of x, is -7.

c, the constant, is -20.

Make sure that you keep the sign that is in front of each of these numbers.

Next we will plug it into the quadratic formula. Note that we are only plugging in numbers, we don't also plug in the variable.

Step 4: Plug the values found in step 3 into the quadratic formula

AND

Step 5: Simplify if possible.

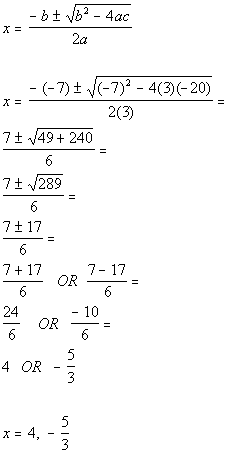*Quadratic formula

*Plug in values found above for a, b, and c

*Simplify

Answer/Discussion to 5a

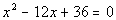
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form, 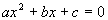, if needed.

This quadratic equation is already in standard form.

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 1.

b, the number in front of x, is -12.

c, the constant, is 36.

Make sure that you keep the sign that is in front of each of these numbers.

Step 4: Plug the values found in step 3 into the discriminant, ,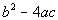

AND

Step 5: Simplify if possible.

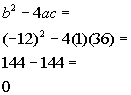*Discriminant formula

*Plug in values found above for a, b, and c

*Discriminant

Since the discriminant is zero, that means there is only one real number solution.

Answer/Discussion to 5b

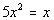
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form, 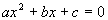, if needed.

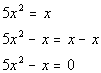*Inverse of add. x is sub. x

*Quad. eq. in standard form

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 5.

b, the number in front of x, is -1.

c, the constant, is 0.
Note that since the constant is missing it is understood to be 0.

Make sure that you keep the sign that is in front of each of these numbers.

Step 4: Plug the values found in step 3 into the discriminant, ,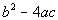

AND

Step 5: Simplify if possible.

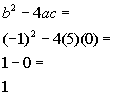*Discriminant formula

*Plug in values found above for a, b, and c

*Discriminant

Since the discriminant is a positive number, that means there are two distinct real number solutions.

Answer/Discussion to 5c

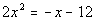
Step 1: Simplify each side if needed.

This quadratic equation is already simplified.

Step 2: Write in standard form, 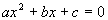, if needed.

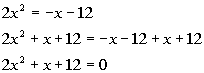*Inverse of sub. x and 12 is add. x and 12

*Quad. eq. in standard form

Step 3: Identify a, b, and c.

a, the number in front of x squared, is 2.

b, the number in front of x, is 1.

c, the constant, is 12.

Make sure that you keep the sign that is in front of each of these numbers.

Step 4: Plug the values found in step 3 into the discriminant, ,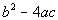

AND

Step 5: Simplify if possible.

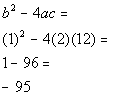*Discriminant formula

*Plug in values found above for a, b, and c

*Discriminant

Since the discriminate is a negative number, that means there are two distinct complex imaginary solutions.

All contents
July 7, 2002