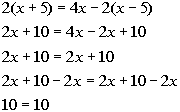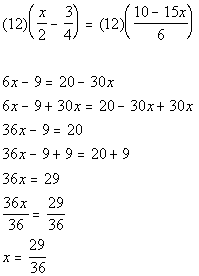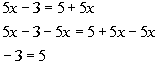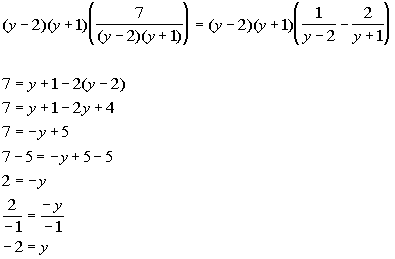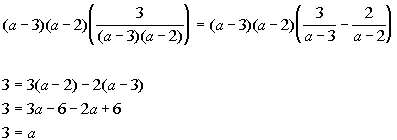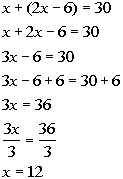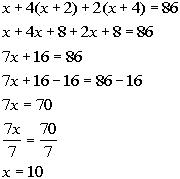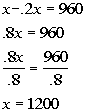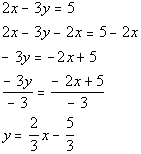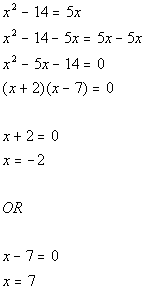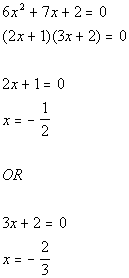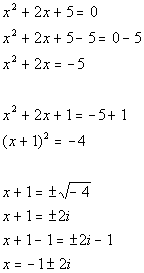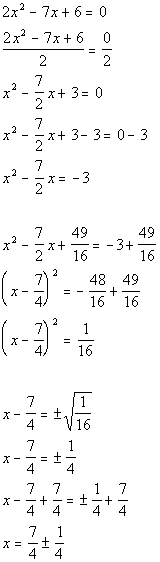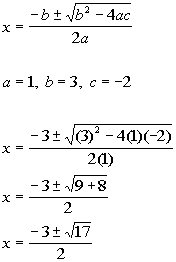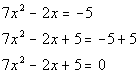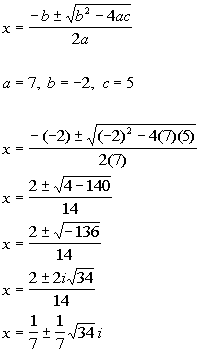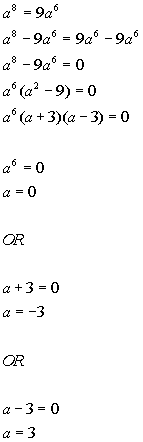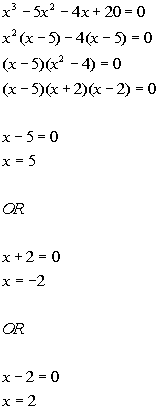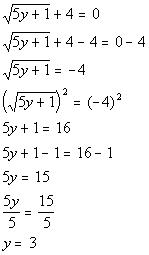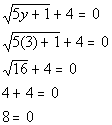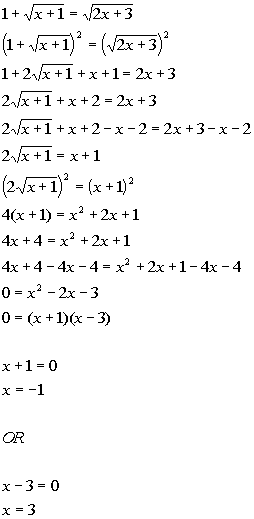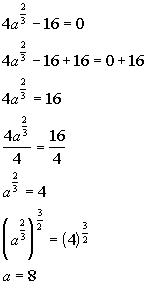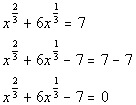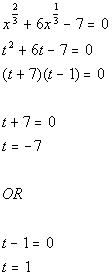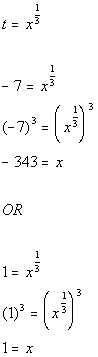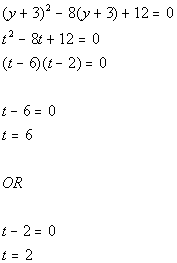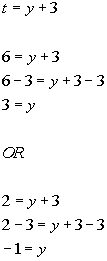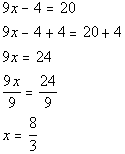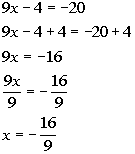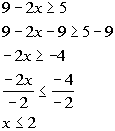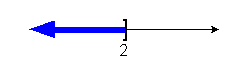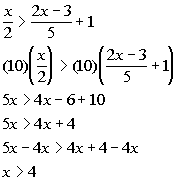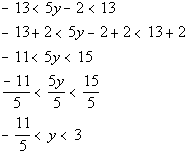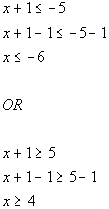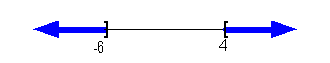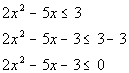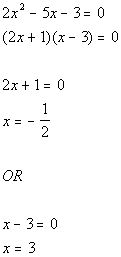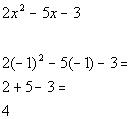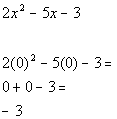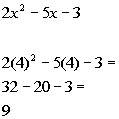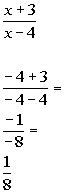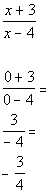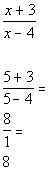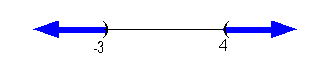College Algebra
Answer/Discussion to Practice
Test
| Problems 1a - 1c: Solve the given equation and determine whether
the equation is an identity, a conditional equation or an inconsistent
equation. |
| Problems 2a - 2b: Solve the given equation. |
2a. 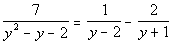
 Answer: Answer:
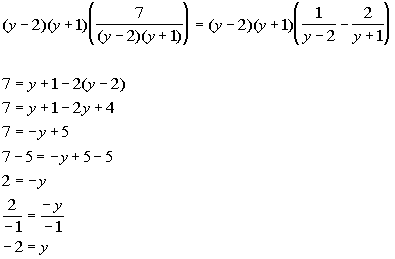
Note that -2 does not cause any denominators to be zero. So it
is not an extraneous solution.
-2 is the solution to our equation. |
|
2b. 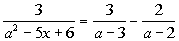
 Answer: Answer:
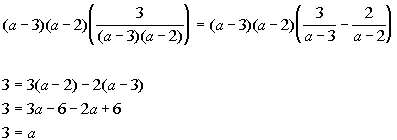
Note that 3 does cause two of the denominators to be zero.
So 3 is an extraneous solution. That means there is no solution.
The answer is NO solution. |
|
| Problems 3a - 3c: Solve the given word problem. |
3a. In last weeks football game, Ralph scored 6 less than twice what
Tommy scored. The sum of their scores is 30. How many points
did Ralph and Tommy score individually?
 Answer: Answer:
Assign variable:
x = Tommys
score
2x - 6 = Ralphs
score
Since their sum is 30, we get the following
equation:
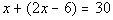
Solving the equation we get:
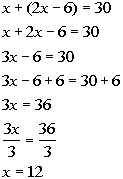
Answer:
Tommy scored 12 points.
Ralph scored 2(12) - 6 = 18 points. |
|
3b. The ages of three sisters are three even consecutive integers.
If the sum of the 1st, four times the 2nd, and twice the 3rd is 86, what
are the three ages?
 Answer: Answer:
Assign variable:
x = 1st even consecutive
integer
x + 2 = 2nd even
consecutive integer
x + 4 = 3rd even
consecutive integer
Since the sum of the 1st, four times the 2nd,
and twice the 3rd is 86, we get the following equation:
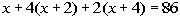
Solving the equation we get:
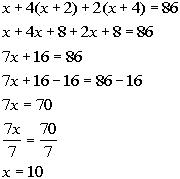
Answer:
The three ages are 10, 12, and 14. |
|
3c. You are buying a computer at a markdown price of $960.
If the markdown price was 20% of the original price, how much was the computer
originally?
 Answer: Answer:
Assign variable:
x = original price
Since the markdown price is $960, we get the
following equation:
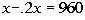
Solving the equation we get:
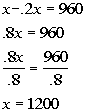
Answer:
The original price of the computer is $1200. |
|
| Problem 4a: Solve for the given variable. |
| Problems 5a - 5b: Solve the given equation by factoring. |
| Problems 6a - 6b: Solve the given equation by completing the
square. |
| Problems 7a - 7b: Solve the given equation by using the quadratic
equation. |
| Problems 8a - 8b: Solve the given equation by factoring. |
| Problems 9a - 9b: Solve the given equation. |
9a. 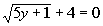
 Answer: Answer:
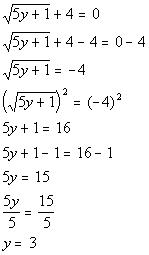
Checking for extraneous solutions:
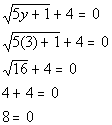
Since we got a false statement, y = 3 is
an extraneous solution.
This means there is no solution to this equation. |
|
9b. 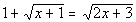
 Answer: Answer:
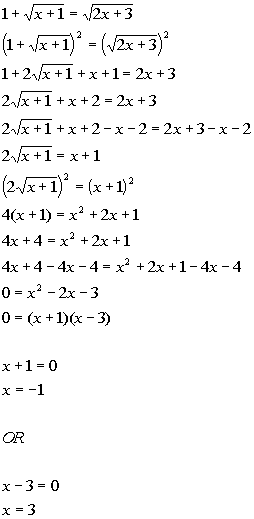
Both x = -1 and x
= 3 check.
There are two solutions to this equation: x
= -1 and x = 3. |
|
| Problem 10a: Solve the given equation. |
10a. 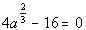
 Answer: Answer:
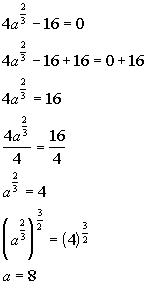
a = 8 does check.
There is one solution to this equation: a
= 8. |
|
| Problems 11a - 11b: Solve the given equation. |
11a. 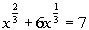
 Answer: Answer:
Writing the equation in standard form:
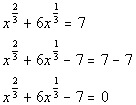
Substitution:
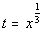
Substitute in t and solve:
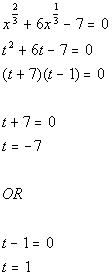
Substitute value in for t and solve for
x:
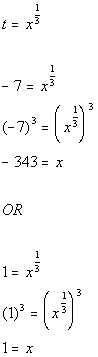
There are two solutions to this equation: x
= -343 and x = 1. |
|
11b. 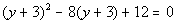
 Answer: Answer:
Substitution:
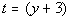
Substitute in t and solve:
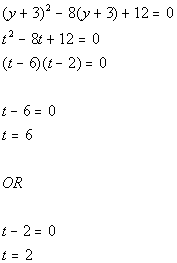
Substitute value in for t and solve for
y:
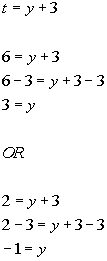
There are two solutions to this equation: y
= 3 and y = -1. |
|
| Problems 12a - 12b: Solve the given equation. |
12a. 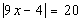
 Answer: Answer:
First solution:
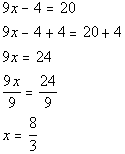
Second solution:
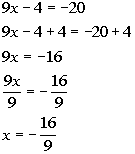
There are two solutions to this equation: x
= 8/3 and x = -16/9. |
|
12b. 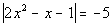
 Answer: Answer:
Since the absolute value is set equal to a
negative number, there is no solution. |
|
| Problems 13a - 13b: Solve, write your answer in interval notation
and graph the solution set. |
13a. 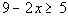
|
13b. 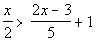
|
| Problems 14a - 14d: Solve, write your answer in interval notation
and graph the solution set. |
14c. 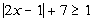
 Answer: Answer:
Isolate the absolute value:
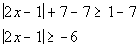
Since the absolute value is ALWAYS positive and in this problem it is
set greater than or equal to a negative number, the answer is all real
numbers. |
|
14d. 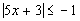
 Answer: Answer:
Since the absolute value is ALWAYS positive and in this problem it is
set less than a negative number, the answer is no solution. |
|
| Problems 15a - 15b: Solve, write your answer in interval notation
and graph the solution set. |
All contents
August 25, 2002 |