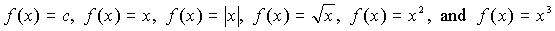SOLVE AND GRAPH NON LINER SYSTEM OF EQUATIONS

simplifying square roots with exponents ,   solved sample papers for class viii of chapter square and square roots,   simplifying radical expressions solver , difference between evaluation & simplification of an expression,   solving second order non homogeneous differential equations ,   quadratic equations vertex and standard form online calculators ,    algebra 2, vertex form of a linear equation ,   interactive games solve a quadratic equation by completing the square , solve non homogeneous first order partial differential equation ,     integer adding,subtracting,multiplying, dividing worksheet , symbolic method math formula solving, calculator texas instruments convert decimals into fractions , simultaneous equation solver quadratic 3 unknowns ,   maths, algebra balancing linear equations, solving simultaneous nonlinear equations matlab ,     ways to cheat on dividing a decimal by a whole number ,   Educational games solve a quadratic equation by completing the square ,   square root simplify equations calculator , how to calculate greatest common divisor ,   convert decimal to radical fraction expression,   finding the least common denominator algebra , factor calculator for a quadratic equation ,     factoring a difference of squares lesson plan for algebra 2 , square root calculator using simplified radical ,   solving linear equation cheats ,   factor polynomial college algebra two variable ax by , Solving Non linear differential equations ,       writing linear equations powerpoint presentation , exponent definition quadratic hyperbola parabola ,   a help sheet explaining how to solve equations by balancing them ,     easy addition and subtraction of algebraic expressions , Solving simultaneous algebra equations
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solve and graph non liner system of equations, here's the result:

---

Understand the Cartesian coordinate system and the idea of locating ordered pairs of numbers. Know and use the mid-point and distance formulas to solve real world problems. Know how to graph relations in the coordinate plane. Find domain and range of a relation from a list or ordered pairs, graph or a table of values. Recognize and evaluate basic features of a graph of a relation. Produce graphs of simple relations using tables. Find the x and y-intercepts of the graph of an equation (algebraically and graphically) Determine the symmetry of the graph of an equation (algebraically and graphically) Write the General Form Equation of a circle in Standard Form and determine the center and radius of the circle

Basic Features of a Graph domain and restricted values range x and y intercepts intervals where a graph is constant, increasing or decreasing

Linear Equations and Inequalities

1. Solve linear equations algebraically and graphically.
2. Deal with fractional coefficients in equations.
3. Solve equations involving absolute value algebraically.
4. Solve a formula for a given variable.
5. Solve word problems by setting up and solving a linear equation in one variable.
6. Solve linear inequalities in one variable including compound inequalities and inequalities involving absolute value algebraically.
7. Represent (graph or plot) solution sets of inequalities on the number line.

Quadratic Equations

Solve quadratic equations by a variety of methods. Use the discriminant to understand when a quadratic has no, one or two real roots algebraically. Solve simple word problems using quadratic equations Construct and use a quadratic model to solve an application problem

Methods of Solving Quadratics By factoring and Using Zero Factor Property when possible. By extracting square roots By completing the square Using the Quadratic formula

Polynomials and Polynomial Expressions

Perform basic operations with polynomials (add, subtract, multiply including FOIL) Use formulas for these special products: Factor polynomials by factoring out the Greatest Common Factor, by grouping, and by using special products formulas for trinomials Factor simple trinomials of form a x2 + b x + c by guess-and-check or by grouping Solve simple equations using the Zero Factor Property when possible. Solve polynomial inequalities (degree > 1)

The Special products: (a + b)2 (a - b)2 (a + b)(a - b)

Solving Non-linear Inequalities Use critical numbers to determine test intervals for a polynomial inequality Solve a polynomial inequality algebraically and graphically Construct and use a polynomial inequality to solve an application problem

Rational Expressions

1. Know how to decide the domain of a rational expressions. (Decide what values are excluded by the denominator.)
2. Simplify and perform basic operations involving rational expressions (addition, subtraction, multiplication, division)
3. Find a Least Common Denominator and use it to add or subtract rational expressions.
4. Solve equations with rational expressions. Recognize that some solutions may be extraneous and check for that.
5. Within the context of sections covered, apply rational expressions to simple situations.

Other Types of Equations and Inequalities

1. Solve equations involving radicals or rational exponents
2. Solve equations involving rational fractions
3. Solve equations involving absolute values
4. Solve higher degree polynomial equations by factoring
5. Solve equations methods as appropriate.

Equations of the Line and Linear Inequalities

	Representations of a line: Standard form: A x + B y = C where A, B, and C are any real numbers. Slope-intercept form: y = m x + b where m is the slope of a line and b is the y-intercept. Point-slope form: y - k = m (x - h) where (h,k) is any point on the line.
	Special Slope Relationships. Horizontal lines (m = 0) Vertical lines (m is undefined) Parallel lines (m1 = m2) Perpendicular lines (m1 m2 = -1)

General Function Concepts

Definition and Notation

1. Determine if an equation or a set of ordered pairs represents a function
2. Use function notation
3. Evaluate a function
4. Find the domain of a function
5. Create and apply a piecewise-defined function.
6. Interpret input and output of real-life functions
7. Solve an application problem involving real-life functions

Graphs of functions

1. Find domain and range using the graph of a function
2. Vertical Line Test
3. Describe the increasing and decreasing behavior of a function
4. Classify a function as even or odd
5. Identify six common graphs

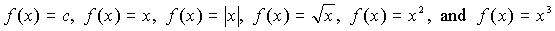
Transformations of Functions

1. Sketch the graph of a function using common graphs and transformations
2. Write the equation of function using common graphs and transformations

Algebra of Functions

1. Find the sum, difference, product, and quotient of functions
2. Find the composition of two functions and determine the domain and range
3. Identify a function as the composition of two functions
4. Solve real-life problems involving combinations and composition of functions

Inverse Functions

1. Determine if a function has an inverse function (Horizontal Line Test)
2. Find the Inverse of a function
3. Graph a function and its Inverse (Know that the graph of f ^-1 is a reflection of the graph of f across the line y = x.)

Polynomial Functions

Polynomial division

1. Divide polynomials using long division
2. Divide polynomials using Synthetic division
3. Use the Remainder Theorem to evaluate a polynomial
4. Use the Factor Theorem to factor a polynomial

Complex numbers (if covered by your instructor)

1. Perform operations with complex numbers and write the results in standard form
2. Solve a quadratic equation involving complex zeros

Polynomial analysis

Rational Functions

1. Find the domain of a rational function
2. Find the vertical and horizontal asymptotes of the graph of a rational function
3. Sketch the graph of a rational function
4. Use a rational function model to solve an application problem

Exponential Functions

1. Sketch the graph of an exponential function
2. Investigate basic characteristics of an exponential function (domain, range, intercepts, increasing/decreasing behavior)
3. Write formulas of transformed exponential functions
4. Use an exponential model to solve an application problem (in particular, models involving the natural exponential function)
5. Use the compound interest formula to solve finance problems
6. Construct and use a model for exponential growth or exponential decay

Logarithmic Functions

1. Properties of logarithms
2. Solve Logarithmic and Exponential Equations
3. Sketch the graph of a logarithmic function
4. Investigate basic characteristics of a logarithmic function (domain, x-intercept, vertical asymptote)
5. Write formulas of transformed logarithmic functions
6. Use a logarithmic model to solve an application problem (in particular, models involving the natural logarithmic function)

Systems in two variables

Solve a linear system of equations Construct and use a linear system of equations to solve an application problem Solve nonlinear systems Construct and use a nonlinear system of equations to solve an application problem

Methods of Solving Systems. by substitution by elimination graphically