Thank you for visiting our site! You landed on this page because you entered a search term similar to this: a help sheet explaining how to solve equations by balancing them, here's the result:
Though this student made a mistake on the first line, her logic was perfect. She started out with one nickel, which meant she needed 5 dimes (4 more). By multiplying the number of nickels by 5 and adding this value to the product of the number of dimes and 10, she was able to obtain her total. Using guess and check, she continued to increment her values for nickels until she arrived at a total of $1.15.
Four of the 6th graders obtained the correct solution to this problem. Each was able to explain his or her work well, and their strategies remained fairly consistent throughout the problem-solving sessions.
8th Grade Responses:
To my surprise, the 8th graders showed the most difficulty with this problem. Each student started out using systems of equations to model the problem. Four of the five algebra students developed a version of the following system:
N = nickels, D = dimes
D = N + 4
N + D = 115
Problem #1 was consistently the most difficult and time consuming for the 8th graders, partly because of their stubborn efforts to force the problem to work. When I asked one stumped student what her equations meant, she replied, I dont know! I just put them down! These students could not explain their work well. To provide insight into the struggles on this problem, consider this 8th grade (who maintains an A in the class) students work:
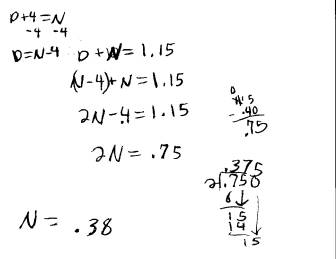
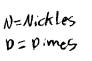
From the beginning, she incorrectly set up her systems by defining the equation:
D + N = 1.15.
Her problems only became worse. Using the method of substitution, she replaced D with (N-4), only to realize that she had a decimal value on one side of the equation and a whole number on the other side. She realized that this was a problem, but simply added a decimal in front of the 4. She had no concept of what these values represented or even what her equations meant. Though she repeated her calculations several times, she could not get a satisfactory result. So she tried a different approach:
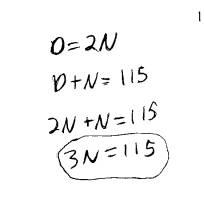
She knew that the value of a dime is equal to two nickels. Thus, she replaced her N = D+4 equation with D=2N. It seems clear that she also has little understanding of her variable meanings. In the same system, D stands for a monetary value $0.10 as well as the number of dimes. Once again, she could not explain her work well, and in the end obtained the correct answer using guess and check methods.
The other students displayed similar difficulties, although one of the four eventually remedied her mistake. Three of the five total students reverted to guess and check to obtain their final solution.
Problem #2:
1. Elinor loves to paint. She paints pictures to sell in her mothers store. She earns $3 for her small paintings and $5 for her large paintings.
a. How much money would Elinor earn if she sold 6 large paintings and 11 small paintings?
b. One Monday, Elinor sold only small paintings. She earned $36. How many small paintings did she sell?
c. On Tuesday, Elinor sold 3 more large paintings than small paintings. In total, she earned $39. How many of each size painting did she sell?
This example produced results very similar to the first problem. Each student was able to solve parts (a) and (b) successfully or with only insignificant arithmetic errors. Part (c) proved the most challenging.
6th Grade Responses:
Again, the 6th grade students utilized guess and check methods to solve this problem. Several used charts to organize their work, one would write an answer and erase it until he found the correct solution, and one student was unable to solve the problem. The techniques were very similar to the first problem.
8th Grade Responses:
Again, only one algebra student successfully used algebra to solve part (c). The other students set up the system with the same error:
S = Small, L = Large
S + L = 39
L = S + 3
These students eventually solved the problem using guess and check methods.
Problem #3:
Arwen wants to plant a tulip garden. To keep out the rabbits, she must set up a fence around the flowerbed. She has 24 feet of fencing.
a. If Arwen makes a square flowerbed with her fencing, how long will each side be? What is the area of this flowerbed?
b. In the square flowerbed, Arwen wants to plant 2 tulips for every square foot inside the flowerbed. How many tulips will she plant in the flowerbed from part(a)?
c. Arwen decided to make the flowerbed a rectangle. She made one side 4 feet longer than the other side. How long is each side of her flowerbed?
This problem is geometry-based but can be solved algebraically. Surprisingly, only half the students drew a diagram while working on this problem. Most students had little trouble with parts (a) and (b) outside of an occasional lack of conceptual understanding of area and perimeter. Again, the most interesting part of Problem #3 was part (c).
Each student that drew a picture also employed the guess and check method. Most of these students used charts; one student drew the rectangles to scale using a ruler and 1 inch = 1 foot. One 6th grade student was quick to solve this style of problem in the previous two algebraic examples, but had difficulty seeing any relationship between those problems and this geometry problem. In the end, she was successful, but could not see the same algebraic relationships that she had used in the previous problems.
Only two of the students missed this problem. The first was the 6th grade student who was unable to understand any of the previous similar situations. Ironically, the second was the only student who set up the problem correctly using algebraic methods. Each of the other students used guess and check methods to obtain their solutions. The algebra students again set up the system incorrectly, and one did not even attempt to use algebra by this point.
This is an example of the correct system of equations used by an 8th grade student:
