Thank you for visiting our site! You landed on this page because you entered a search term similar to this: how to calculate greatest common divisor. We have an extensive database of resources on how to calculate greatest common divisor. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
FSM + D: Greatest Common Divisior
I. Introduction
The purpose of this lab is to implement a finite state machine in VHDL to calculate the Greatest Common Divisor(GCD) of 2 numbers.
The algorithim used to compute the GCD is as follows. Two numbers
are compared ( x = y ?). If so the the GCD is found. If x > y,
then x = x - y. The two numbers are then compared once again. If y >
x, then y = y - x. The two numbers are then compared once again. Here
is and example of our algorithim:
x = 10
y = 2
Is x = y? No, x > y therefore x = x - y
in our case, x = 10 - 2 = 8.
Is x = y? No, x > y therefore x = x - y
In our case, x = 8 - 2 = 6.
Is x = y? No, x > y there fore x = x - y
In our case, x = 6 - 2 = 4.
Is x = y? No, x > y therefore x = x - y
In our case, x = 4 - 2 = 2.
Is x = y? Yes, therefore the GCD of 10 and 2 is 2.
Note that 0 is not a valid input.
The design of the GCD calculator should be divided into 2 parts - a controller and a datapath. The controller is an FSM which issues commands to the datapath based on the current state and the external inputs. This can be a behavioral description. The datapath contains a netlist of functional units like multiplexors, registers, subtractors and a comparator, and hence this design is structural. The controller basically steps through the GCD algorithim shown above. If x = y, we have finished computing the GCD, and we go to the final state and assert the data output line. The Datapath does the actual GCD computation. It has the following components:
- Mux: takes 2 4-bit inputs and one select line. Based on the select line, it outputs either the 1st 4-bit number or the 2nd 4-bit number.
- Register: Takes a 4-bit input, a load signal, reset, and a clock signal. If the load signal is high and the clock is pulsed, it outputs the 4-bit number.
- Comparator: Takes 2 4-bit numbers, and assets one of 3 signals depending on whether the 1st number is less than, greater than or equal to the 2nd number.
- Subtractor: Takes 2 4-bit numbers, subtracts the smaller number from the larger.
- Output Register: Holds the GCD value. When x = y the GCD has been found and can be outputted. Because it is a register entity it should also take a clock and reset signal.
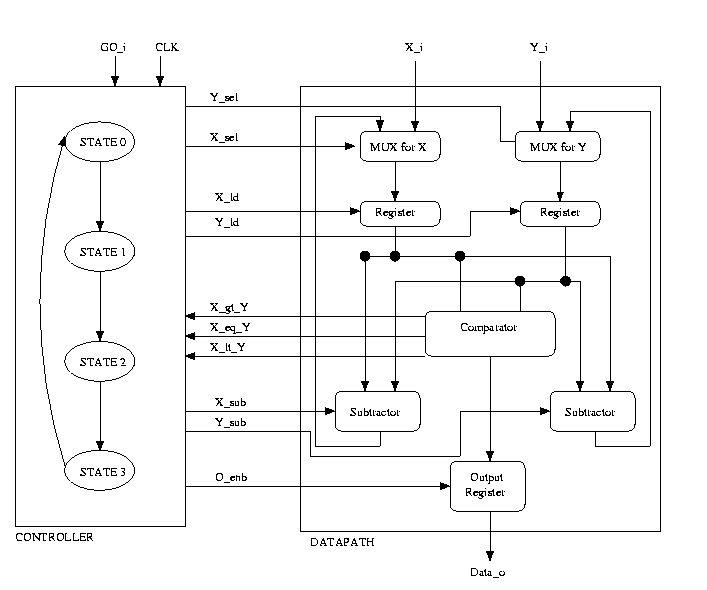
Sample Structure of the Controller and Datapath
II. Procedure
implementation and simulation:
- For an idea of how the gcd calculator might look, refer to the above figure. However, you state machine can have a different number of states, archs, and loops.
- Create an FSM to reflect the GCD calculation process.
- Convert the FSM to an FSM +D
- Write the VHDL code to reflect the controller and data path.
- Write a test bench and verify the correctness of your design using Aldec Active-VHDL
- Once you have verified your results using Aldec HDL, check out an XS40 board from the T.A.
- You will need to add the 7-segment decoder to the design.
- Create a .ucf file to reflect your connections and generate a bit file.
- Download your .bit file and verify your results.