Thank you for visiting our site! You landed on this page because you entered a search term similar to this: square root calculator using simplified radical. We have an extensive database of resources on square root calculator using simplified radical. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
Prerequisites
It is assumed that you know the following material coming into the College Algebra course. Please bring yourself up to date if you do not.
Interval Notation
An alternative form of expressing inequalities is to use interval notation. Interval notation consists of two values, separated by commas.
The first value is the left hand endpoint of the interval, and the second value is the right hand endpoint of the interval. The left hand endpoint is always on the left, and the right hand endpoint is always on the right. If the inequality extends forever in the negative direction, then the left hand endpoint should be negative infinity. If the inequality extends forever in the positive direction, then the right hand endpoint should be positive infinity.
Each endpoint is surrounded by either a bracket [ ] or parenthesis ( ). The left hand
endpoint is proceeded by a left bracket [ or left parenthesis ( and the right hand
endpoint is followed by a right bracket ] or right parenthesis ). A bracket means the
endpoint is included and a parenthesis means the endpoint is not included.
Infinity (positive or negative) is never included and should always be enclosed with a
parenthesis.
An open interval is when both endpoints are not included ( ). A closed interval is when both endpoints are included [ ]. A half-open (or half-closed if you're a pessimist) interval is when one endpoint is included and the other endpoint isn't ( ] or [ ).
Examples of Interval Notation
Write: -2 < x < 5 as ( -2, 5 )
Write: -2 <= x < 5 as [ -2, 5 )
Write: x >= 2 as [ 2, +∞ )
Write: x < 5 as ( -∞, 5 )
Absolute Value
Most people know the absolute value of any number to be zero or positive. However, mathematically, it requires a piecewise definition.
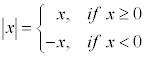
When working with absolute values, this means that to remove an absolute value from an algebraic expression, the absolute value expression must be replaced with two cases. One case is obtained by simply dropping the absolute value signs and leaving the argument. The other case is obtained by taking the opposite of the argument of the absolute value function. Each case is then worked out individually.
Sometimes, it will be possible to solve an equation involving absolute values by using a plus-minus when eliminating the absolute value signs. Be careful doing this, and if you have difficulty, then revert back to the two separate cases.
Another way to eliminate an absolute value is to square both sides of the equation. Taking the absolute value makes things non-negative, and squaring makes things non-negative. So, if you square something, you no longer need to take its absolute value. However, be careful when squaring both sides of an equation as this can lead to extraneous solutions.
Field Properties of Real Numbers
- Closure Property - The sum or product of any two real numbers is another real number.
- Commutative Property - The order of the terms or factors can be changed.
- Associative Property - The grouping of terms or factors can be changed.
- Identity Properties - Zero added to any number is that number. One multiplied by any number is that number.
- Inverse Properties - Any number plus its opposite is zero. Any number, except zero, times it's reciprocal is one.
- Distributive Property - Multiplication distributes over addition.
Note that the properties are defined for addition and multiplication. Some of the properties do not work for subtraction or division.
Fundamental Theorem of Arithmetic
Every integer greater than one is either a prime number or can be written as an unique product of prime numbers.
Prime numbers are your friends. Be able to factor numbers using primes, it will make life much easier later on.
Exponents
When multiplying two factors with the same base, add the exponents.
When multiplying two factors with the same exponent, but different bases, multiply the bases and keep the exponent.
When raising to a power, multiply the exponents together.
Scientific Notation
Be able to convert a number from scientific notation into regular notation and from regular notation into scientific notation.
The TI-82/TI-83 calculator uses the EE key as the scientific notation key. When you see a number displayed like 1.253E12, that really means 1.253×1012.
Roots
Know how to convert between radical form and rational exponent form. In rational exponent form, the denominator of the exponent is the index of the root and the numerator is the power of the expression.
For example, x2/3 would be the cube root of x2.
Be careful when taking the nth root of the nth power. If the power is even, then you need to take the absolute value of the base when simplifying the radical.
Simplified Radical Form
A value is in simplified radical form when the following conditions are met.
- The exponents on all prime factors in the radicand must be less than the index of the radical. Basically, that means you can't have the square root of x3.
- No fractions in the radicand.
- No radicals in the denominator.
- No common factors between the exponent on a prime factor in the radicand and the index of the radical. This means that you should reduce your index and power if possible.
Factoring Polynomials
Know the special cases of the difference of two squares, the sum of two squares (which is prime over the reals and doesn't factor), the difference of two cubes, the sum of two cubes, and the difference of two nth powers.
- Difference of two squares: x2 - y2 = ( x - y ) ( x + y )
- Sum of two squares: x2 + y2, doesn't factor over the reals
- Difference of two cubes: x3 - y3 = ( x - y ) ( x2 + xy + y2 )
- Sum of two cubes: x3 + y3 = ( x + y ) ( x2 - xy + y2 )
- Difference of two nth degree terms: xn - yn = ( x - y ) (xn-1 + xn-2y + ... + xyn-2 + yn-1 )
The above are really patterns to use as guidelines. For example, 4x2-25 is the difference of two squares. Some specially crafted sum of squares will factor but that is beyond what I expect you to know for this course.
Know how to factor a trinomial that isn't a special case. You might find the AC method of factoring to be beneficial in this case.
Know how to factor by grouping.
Special Products
Know the square and cubes of a binomial.
- A sum squared: ( x + y )2 = x2 + 2xy + y2
- A difference squared: ( x - y )2 = x2 - 2xy + y2
- A sum cubed: ( x + y )3 = x3 + 3x2y + 3xy2 + y3
- A difference cubed: ( x - y )3 = x3 - 3x2y + 3xy2 - y3
These are special cases of something known as the binomial expansion theorem that will be covered in section 7.5.
Fractional Expressions
Expressions don't have equal signs. If they did, they would be equations. When there is no equal sign, you cannot multiply both sides of the equation (because there is no equation) by the least common denominator and eliminate the denominator.
What that means is that when working with rational (fractional) expressions, you will have a denominator in the final answer (unless it happens to divide out with a factor in the numerator).
You divide out or reduce factors in the numerator with factors in the denominator. Do not cancel (unless you want to see the instructors blood boil). Do not divide out individual terms (factors are multiplied together, terms are added together).
With compound fractions involving monomials, you may invert and then multiply.
However, when there are polynomials in the compound fraction, it is generally easier to multiply the top fraction and bottom fraction by the least common denominator of the two denominators.
Cartesian Plane
Be able to construct a Cartesian Coordinate System. This is also known as the x-y coordinate plane. Know the names of the quadrants. Be familiar with the concept of an ordered pair and be able to plot points on the system given its coordinates.
The x-coordinate is also known as the abcissa and the y-coordinate is also known as the ordinate.
Formulas
You should know the following formulas.
- The distance between two points. This is basically just Pythagorean's Theorem. Find the change in the x-coordinates and the change in the y-coordinates. Square each of them and add them together. Finally, take the square root.
- The midpoint formula. The midpoint between two points is found by adding together the x's and dividing by 2 and adding together the y's and dividing by 2.
- The equation of a circle with center (h,k) and radius r. (x-h)2 + (y-k)2 = r2
Exploring Data
You are not responsible for this section of the book. However, it is strongly urged that you read through the material and become comfortable with it. We will be using it quickly in chapter 1. Some good notes on how to use the calculator for data exploration is available in the TI-82 and Statistics sections of the online notes.
Table of Contents: College Algebra Notes
James Jones website