distributions,partial differential equations ,    greatest common divisor calculator ,    online factoring of complex quadratic equations with variables only , free advanced algebra add subtract rational expressions,   how do you do the square root on the TI-83 plus graphic calculator?,   Like Terms Simplifying Algebraic Expressions Activities Lessons,  adding subtracting dividing multiplying integers games ,   solving quadratic equations completing the square, pre-algebra ratio formula , how do you divide and times add subtract integers worksheet ,   multiplying and dividing powers cheat ,  solving multiple variable polynomial equation ,   practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade,    simplifying exponents and square root calculator , quadratic equation extracting square root , how do i convert a basic algebraic equation, difference between evaluation and simplification of an expression, convert decimal to square root fraction ,  multiply and divide rational expressions calculator ,greatest common factor for three number with variables ,   adding, subtracting, multiplying, dividing integers, adding subtracting multiplying dividing integers, worksheet on adding,subtracting,multiplying,dividing integers , calculate greatest common divisor ,    Adding, subtracting, multiplying and dividing Integer worksheets , worksheets on add subtract multiply divide fractions,    quadratic equations square root property calculator ,  Simplifying a sum of radical expressions calculator ,    simplifying cube root fractions,    prealgebra solving equations by multiplying and dividing worksheet,  solving addition and subtraction equations worksheet , simultaneous nonlinear equation solver,  Like Terms Simplifying Algebraic Expressions Junior High, value for variable expression radicals roots ,    adding and subtracting fractions with like denominators worksheet ,    how use my Casio Calculator for solving linear equations,  multiplying,dividing,adding,subtracting integers,  converting base 8 to decimal calculator,  solving 2nd order differential equations, Java method Convert Decimal Numbers to time ,    quadratic equation graph hyperbola ,     simplify square root of difference of two squares , integers adding, subtracting, multiplying, dividing worksheet  
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: finding least common denominator to equations.We have an extensive database of resources on finding least common denominator to equations. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!

---

Math 121 Hints & Examples

Word Problems

Solving Equations

Question: Solve each Equation
Tip: Solve the equation means isolate the variable.

Example:
4/y - 5 = 5/2y
Lets get rid of the fraction by finding a LCD (Least Common Denominator). Since y is common to 2y, the LCD is 2y.
2y(4/y) - 2y(5) =2y(5/2y)
We can get rid of the Common Denominator since we are in an equation.
8 - 10y = 5
Isolate the variable (y)
-10y = -8 + 5
Divide by -10 on both sides
y=3/10

Question: Solve for indicated variable
Tip: Use the same logic as the previous example; look at the operation performed on the letter you want to isolate and un-do them by their opposites (e.g. divide if the variable you want to isolate is multiplied to a number or a other variable)

Example:
A = P(1 + rt) for r
Tip: The goal is to isolate the letter r. Notice that we are in an equation (this problem would be impossible to do if there is no = sign)
Instead of foiling, we can first divide by P since P is multiplying the expression (1 + rt)
A/P = 1 + rt
A/P 1 = rt
(A/P 1)/t = r (we can re-write this as (A/P 1) X 1/t or A/tP 1/t)

Setting Up Equations

Question:translate each sentence into a mathematical equation. Be sure to identify the meaning of all symbols.
Tip: When solving word problems, read the problem once without writing anything. Read the question twice and define your variable(s) they are always in the question. Then re-read the problem keeping in mind the variable you just defined. There are many ways to solve word problems especially when there is more than one variable..

First Example : A total of $10,000 is to be divided between Sean and George, with George to receive $ 2,000 less than Sean. How much will each receive?

x = the Amount $ that Sean is going to receive
x 2000 = the Amount $ that George is going to receive

Tip: the word divided in this problem is misleading because nothing gets divided.

My equation is x ($ for Sean) + x 2000 ($ for George) = 10000

2x = 12000
x = 6000 (Are you done with the problem? NO This is only saying that Sean is going to get 6000 out of the 10000. This implies that George will get (6000 2000 or $4000)

Second Example: The perimeter of a rectangle is 60 feet. Find its length and width if the length is 8 feet longer than the width.

Tip: Geometry problem will assume that you know the Perimeter formula (P = 2L + 2W) and Area formula (A = LW) for rectangle. Always pick your variable to be what you know least about.

In this problem we know nothing about the width, but a lot about the length. By re-reading the problem, establish the following facts:
Width = x
Length = x + 8
60 = 2(x + 8) + 2(x) and solve for x
60 = 2x + 16 + 2x
44 = 4x
11 = x (Are you done with the problem? NO)
We can say that the width is 11 feet and the length is 11 + 8 = 19 feet.

Mixture Problems:

Example: A nut store normally sells cashews for $4 per pound and peanuts for $1.50 per pound. In order to sell 60 pounds of peanuts, the manager decides to mix the 60 pounds of peanuts with some cashews and sell the mixture for $2.50 per pound. How many pounds of cashews should be mixed with the peanuts? How many pounds are in the mixture?
Tip: The variables should be defined based on the question. The problem asks us how many pounds of cashews. So, let'ss define X to be the amount in pounds of cashews and Y to be the Amount in pounds of the mixture.Since we have two variables, we need two equations to solve the problem. Then we can write the system of equation as follow:
X + 60 = Y
4X + 1.5(60) = 2.50Y
We can now substitute for Y in the second equation:
4X + 90 = 2.5(X + 60)
4X 2.5X = 150 90
1.5X = 60
X = 40
This means that we will mix 40 pounds of cashew with 60 pounds of peanuts to have a 100 pounds of the mixture.
Check: 4(40) + 1.5(60) = 100(2.5)
160 + 90 = 250
250 = 250

Here is an alternative way to do this problem. By only defining X = Amount of Cashew we can write the following equation:
4X + 1.5(60) = 2.5(60 + X)
Then we can solve for X and need not to forget that the question is not only asking about the amount of cashew, but also of the total mixture.

Motion Problem:

Example: A motorboat can maintain a constant speed of 16 miles per hour relative to the water (which moves also). The boat makes a trip upstream to a certain point in 20 minutes; the return trip takes 15 minutes. What is the speed of the current (X)?
Tip: Watch out for the units (hours and minutes are mix in this problem) so 20 minutes = 20/60 (60 minutes in an hour). We can use D=RT formula. However, we do not have the distance and do not need the distance.
We get the following equations
x = speed of current

Travelling Upstream...
d = (16-x)20/16

Travelling Downstream...
d = (16+x)15/20

Since the distances are the same, we can equate the distances:
(16-x)20/16 = (16+x)15/20
Then Solve for X.
Answer: X = 4 mph

Quadratic Equations

Example: Solve the following equations:
Tip: Solving an equation means the same as solving for X, finding the zeros, finding the solution, or finding the X intercepts.

4X + 9 = 12X
First subtract 12x from both sides

4X - 12X + 9 = 0
Look for common terms and divide by them first-in this case, however, we cannot divide. We need to recognize that we need to factor this equation.

We need two numbers that multiply to 36(9x4) and add to -12.
We go through the possibilities of what 36 is made of.
36 = 1 · 36 This will not work because 1 - 36 does not = -12
36 = 2 · 18 This will not work because 2 - 18 does not = -12
but 36 = 6 · 6 and - 6 + - 6 = - 12 so those are the numbers that we will use because we get a negative 12 and a positive 36.

Rewrite -12 as -6-6
4x² - 6x - 6x + 9 = 0 or (4x² - 6x) + (-6x + 9) = 0
Factor as much as possible from each factor.
2x(2x-3) + (-3)(2x-3) = 0
Factor out the common term, 2x-3
(2x - 3)(2x - 3) = 0
2x - 3 = 0
2x = 3
x = 3/2

Simple quadratic word problems:

Example: The area of a rectangular window is to be 360 square centimeters. If the length exceeds the width by 1 centimeter, what are the dimensions?
Tip: Area formula is A = LW. We define the width as our variable (since we know least about it) so we can state that L = W + 1
So we can write the following equations using the area formula:
360 = W (W + 1)
0 = W + W - 360
I need two numbers that multiply to - 360 and that add to one. Use your calculator to explore what two numbers 360 is made of.
Well there are not two numbers that multiply to 360 and add to 1, so we will need to use the quadratic formula, which is:
(NOTE: the "|" takes the place of the square root symbol over the rest of the equation within parentheses)
(- b |b- 4ac) / 2a
a =1 , b= 1 c = -360
(-1 |1 + 1440 )/ 2
W = 18.48 or W = - 19.48
Since we are working one with dimensions, they cannot be negative.
The width has to be 18.48 centimeters.
Now the length should be W + 1 = 18.48 + 1 = 19.48


Sample Problem:

A landscaper, who just completed a rectangular garden measuring 6 feet by 10 feet, orders 1 cubic yard of premixed cement, all of which is to be used to create a border of uniform width around the garden. If the border is to have a depth of 3 inches, how wide will the border be?



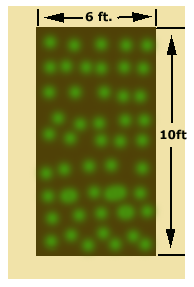
First write the equation you are going to need.
Volume = LWh , Area = LW
Before we can use the volume formula, we need to find the area of the border.
Let's call the area of the garden "G" and the area of the cement border "C", and total area A. Now we say A = G + C or A - G = C. Also, let's call X the two extra distances between 6 and the edge of the border.

C = (6 + 2X)(10 + 2X) - 610
C = 60 + 32X + 4X - 60
C = 32X + 4X = area of the border

Let's convert 3 inches into a foot. 3/12 =
Now we are ready to use the volume formula to fill it in.

Note: 3 feet = 1 yard, (1 yard)³ = (3 feet)³ = 27 feet³

27 (this is the total) = (32X + 4X)
27 = 8X + X
X + 8X - 27 = 0

This is not easily factored by inspection, so we will need to use the quadratic formula (- b |b- 4ac) / 2a where a = 1, b = 8 and c = -27.
(NOTE: the "|" takes the place of the squareroot symbol over the rest of the equation withinparentheses)

(-8 |64 + 108 )/ 2
(-8 |172)/2

We know that the answer cannot be negative so the only possible answer is

X = 2.56