Thank you for visiting our site! You landed on this page because you entered a search term similar to this: quadratic equation graph hyperbola.We have an extensive database of resources on quadratic equation graph hyperbola. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
Education
Equations with Roots 2 and 5:
A Pedagogical Exploration with a Relation Grapher
A Pedagogical Exploration with a Relation Grapher
Let us begin with the simplest case. The pair of functions
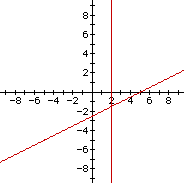
y = x - 5
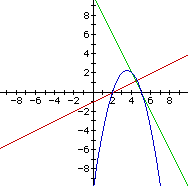
will graph as parallel lines through the points (2,0) and (5,0)with slope of 1.
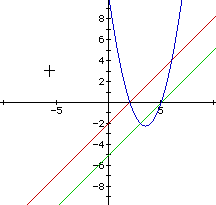
The product of these two functions y = (x - 2)(x - 5) is aparabola also passing through the points (2,0) and (5,0). Thegraph, showing all three functions, is as follows.
The same function is represented by the equation
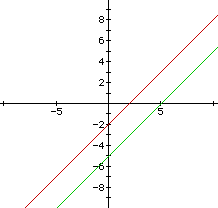
Clearly, we could have started with any two lines through (2,0)and (5,0) respectively, such as
and taken their product
to produce two lines and their corresponding parabola throughthe given points.
Going the other direction, we could take any of the familyof parabolas through the points (2,0) and (5,0) with major axisalong x = 3.5, ,and factor the equation into two linear factorsrepresenting lines through the given points.
Consider again the parabola with the equation
Let us look at rewriting it as
and graphing it. The domain over which the function is definedin the real numbers is restricted to where 7x - 10 > 0. Inthis region, however, the graphs of the two equations are thesame.
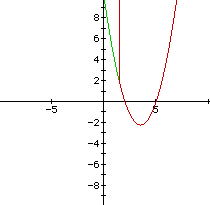
The spurious vertical line results at the boundary of the definedregion -- where 7x-10 approaches zero.
The rewritten equation is in the form of the difference oftwo squares and in factored form we have
That is, we have the function as the product of two functions
and the graph of these two functions (on the same axis) isas follows.
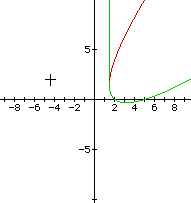
The union of these two graphs appears to be a parabola. Isit? (Again
A single equation for the union of two curves can be found bytaking the product of the relations producing the curves.We set
and simplifying gives
The graph is as follows. This is the equation of a parabolapassing through the points (2,0) and (5,0) having an axis of symmetrywith slope of 1.
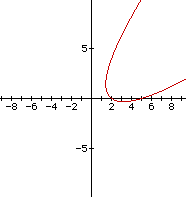
A Different Look
Let us consider again the equation
For any constant a,
is the same graph. Now we have a slightly different way ofputting this in the form of the difference of two squares:
and the factor functions are
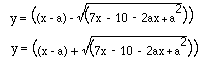
Rewriting as the product of two relations to get the unionof the graphs gives![]()
This simplifies to
Now we can use Graphing Calculator 3.0 to graph a family ofparabolas, all passing through 2 and 5 on the x-axis. The previousparabola graph was the case for a = 0.

a = 0, 1, 2, 3, 4, 5, 6, 7
Perhaps some interesting additional graphs would be betweena = 3 and a = 4. Here are the graphs for a = 3, 3.25, 3.5, 3.75,and 4.
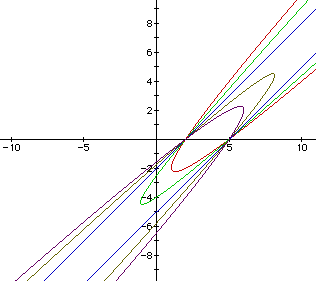
The graph for a = 3.5 deserves a separate look.
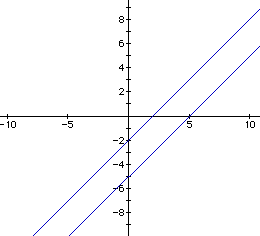
As a approaches 3.5 from below, the family of parabolas allopen upward and become more narrow. As A approaches 3.5 from abovethe parabolas all open downward and become more narrow. At a =3.5, however, the parabola reduces to a pair of parallel lines.This indicates the equation
is factorable. We have
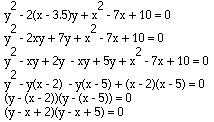
The graph of this relation is a pair of parallel lines. Theseare the lines with which we began this investigation and had wegraphed a product of the two relations
y - x + 5 = 0
we would have obtained the union of the two individual graphs.
There are many parabolas through x = 2 and x = 5 that we havenot yet examined with these equations. For example, what set ofequations would generate the following graphs?
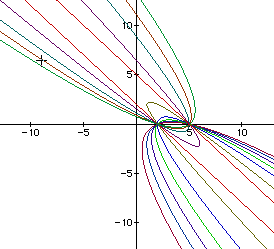
Once Again, Another Approach
If we graph the product
It is clear that the graph will be the parallel lines definedby
and
y - x + 5 = 0
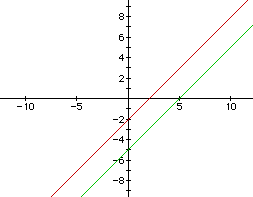
On the other hand, the product
must also produce a pair of parallel lines when it is graphed.This is a generalized quadratic equation of the form
Examination of the generalized quadratic was once standardfare in courses on analytical geometry. Families of graphs areformed by fixing all but one of the parameters and varying theremailing one.
As long as A = 1, C = -7, and F = 10, the graph of
will cross the x-axis at 2 and 5. We know that for particularcoefficients B, D, and E the resulting graphs could be conicsor degenerate conics, that is, conics, circles, or parallel lines.For example, when B = -2, D = 1, and E = 0, the graph is a parabola.
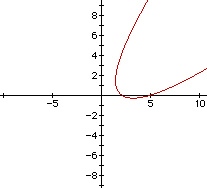
When B = 0, D = 1, and E = -5, for example, the graph is acircle.
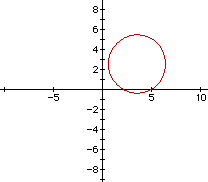
More circles.
Some examples of other figures are
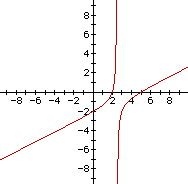
Hyperbolas
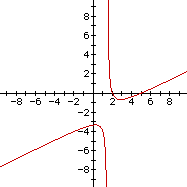
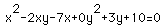
Two Lines
Lines and Hyperbolas
The above three graphs on the same axis shows the two hyperbolasand this pair of lines but the pair of lines can not beasymptotes to either of the hyperbolas since the graphs sharethe points (2,0) and (5,0).
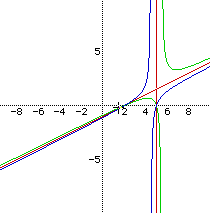
MoreHyperbolas
Ellipses can be formed in several ways. The task here is toshow sets of ellipses through the points 2 and 5 on the x-axis.The general equation is
What values of B, C, and E will give ellipses? Try C = 1 toget the coefficients of the two squared terms equal. Then tryB = 1 and E = 8.
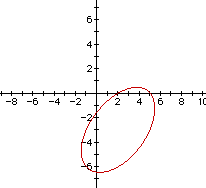
What if C = 1, E is fixed, and B varies?
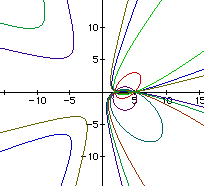
Here we have a rather messy collection of a circle, two ellipses,some parabolas and some hyperbolas, all crossing the x-axis at2 and 5.