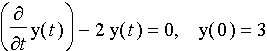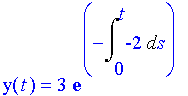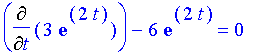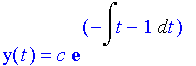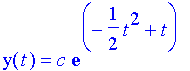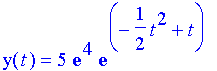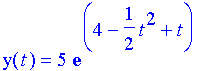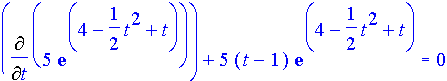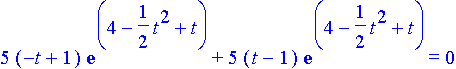Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving second order homogeneous differential equations, here's the result:
First-Order Homogeneous Linear Differential Equations A differential equation that can be written in the form
is called a first-order homogeneous linear differential equation. It's homogeneous because after placing all terms that include the unknown equation and its derivative on the left-hand side, the right-hand side is identically zero for all t. It's linear because y(t) and its derivative both appear "alone", that is, they are not part of any composed function such as
The expression a(t) represents any arbitrary continuous function of t, and it could be just a constant that is multiplied by y(t); in such a case think of it as a constant function of t. What follows is the general solution of a first-order homogeneous linear differential equation. It might seem quite involved, but it is nothing more than one simple step after another. If you don't move on to a next step until you understand the current one, you will have no problem understanding the solution process. The fact that the process is somewhat involved is actually a good thing in our context; once you know how its done, and then see how long Maple takes to do it, you'll be convinced that Maple provides you with tools that really save a lot of time and brain power. Start with
Then
and
Remembering the derivative of the ln function, and using the chain rule,
Thus, by substitution,
Note that we have transformed the original equation into the form discussed at the end of the introduction to differential equations.
So at this point we simply need to integrate both sides of the equation.
Integration and differentiation being inverses of each other, this equation is the same as
The constant comes from the constant produced by the integration of the left side of the equation, and then moving it to the right. Now we need to solve a logarithmic equation, and that involves taking exponents of both sides of the equation.
This equation is the same as
The factor
We have now found an equation that yields y as a function of t, and it would be nice to say that we are finished. But a problem still exists, perhaps even two problems, depending on how you feel about the expression
The bigger problem is that rather than knowing something about the absolute value of the unknown function, we want to say that
Top
(Note: The section designated by the above horizontal line and the next one is provided for completeness. The above equation, with While the following material is essential to justify the removal of the absolute value function, it is not essential to understanding how to execute the solution steps. However, there is one key point that you should know if you skip this section, and that is that the assumption that y(t) is a continuous function is essential to the justification for removing the absolute value function. Also, know that if you skip this section you are missing out on a good example of the use of some basic theorems of calculus to make an interesting argument. to skip the justification and continue with the rest of this introduction to first-order homogeneous linear differential equations.) To justify this step, first make the following change (for reasons you'll see in a second, let's revert back to
Now
A property of the absolute value function says that
By assumption, a(t) is a continuous function of t. A theorem of calculus tells us that if a(t) is continuous, then Now the equation
says that the absolute value of the function
or that
(Note that this conclusion is not necessarily true if the function inside the absolute value function is not continuous. Why? Hint: Define the function f to equal 5 for all In either case, it is certainly true that we can write
where
Finally, this is the general solution of the homogeneous linear differential equation. Note that c is an ancestor of Top
An example: Solve Solution:
becomes
with
Thus, by the formula we just developed,
Which evaluates to
or
As a check, substitute y(t) into the equation and evaluate it.
Which evaluates to
Top
Another example: Solve Solution:
has
Now
And,
Thus,
This simplifies to
Checking our work,
Top
These two examples illustrate how to find the general solution of a homogeneous linear differential equation. However, in most real world situations you generally want one specific solution that depends on certain initial conditions. In these cases you know, or are given, a value
Its solution is as follows. After transforming it into a form that we can integrate, integrate both sides between
becomes
And this becomes
Now take the exponential of both sides.
Following a processes similar to the earlier solution of the absolute value enigma, either
or
To decide this one, note that we already know the value of y(t) for one value of t, namely
Thus, the second option is not possible, and this implies that
Isolate y(t) in this equation to find the general solution of an initial value problem involving a homogeneous first-order linear differential equation.
Top
A couple of examples: Solve Solution: According to the formula,
This evaluates to
As a check,
Which of course simplifies to
Top
Here's another way to solve this kind of initial-value problem. Solve Solution: First solve the equation without concern for the initial condition.
Now solve for c by inserting the known values
Thus,
For this initial condition y(t) is
This simplifies to
A check,
becomes
which simplifies to
The last section that you'll want to read before returning to any polite comments, suggestions, or corrections. |
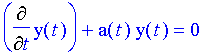
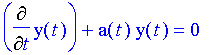
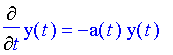
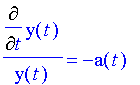
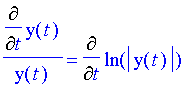
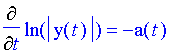

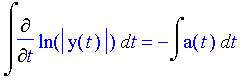
![ln(abs(y(t)))=-int(a(t),t)+C[1]](images-homo14_1.gif)
![abs(y(t))=e^(-int(a(t),t)+C[1])](images-homo15_1.gif)
![abs(y(t))=e^(-int(a(t),t)+C[1]](images-homo16_1.gif)
![C[2]=e^C[1]](images-homo18_1.gif) into the equation.
into the equation. ![abs(y(t))=C[2] e^(-int(a(t),t)](images-homo19_1.gif)
![abs(y(t))=C[2] e^(-A(t))](images-homo25_1.gif)
![y(t)=C[2] e^(-A(t))](images-homo26_1.gif)
![abs(y(t)) e^(int(a(t),t)=C[2]](images-homo28_1.gif)
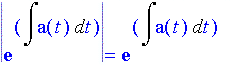
![y(t) e^(int(a(t),t))=C[2]](images-homo32_1.gif)
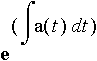 is a continuous function of t. And still yet another continuity theorem assures us that the product of two continuous functions is also continuous. Since the function we're looking for, y(t), is assumed to be continuous, this implies that
is a continuous function of t. And still yet another continuity theorem assures us that the product of two continuous functions is also continuous. Since the function we're looking for, y(t), is assumed to be continuous, this implies that 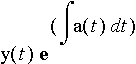 is a continuous function of t.
is a continuous function of t. ![y(t) e^(int(a(t),t))=C[2]](images-homo36_1.gif)
![-y(t) e^(int(a(t),t))=C[2]](images-homo39_1.gif)
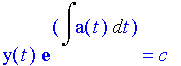
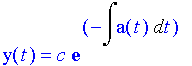
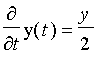 for y(t).
for y(t).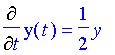
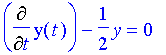
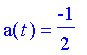
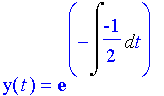
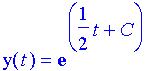
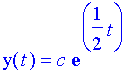
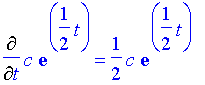
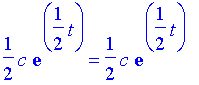
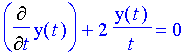
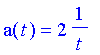
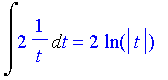
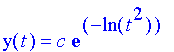
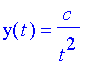
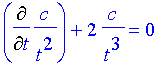
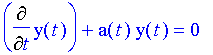
![int(d/dt ln(abs(y(s))),s=t[0]..t)=-int(a(s),s=t[0]..t)](images-homo75_1.gif)
![ln(abs(y(t)))-ln(abs(y(t[0])))=-int(a(s),s=t[0]..t)](images-homo76_1.gif)
![ln(abs(y(t)/y[0]))=-int(a(s),s=t[0]..t)](images-homo77_1.gif)
![abs(y(t)/y[0])=e^(-int(a(s),s=t[0]..t))](images-homo78_1.gif)
![(y(t) e^(int(a(s),s=t[0]..t))/y[0])=1](images-homo79_1.gif)
![(y(t) e^(int(a(s),s=t[0]..t))/y[0])=-1](images-homo80_1.gif)
![(y(t[0]) e^(int(a(s),s=t[0]..t[0]))/y[0])=1](images-homo82_1.gif)
![y(t)=y[0] e^(-int(a(s),s=t[0]..t))](images-homo84_1.gif)