HOW TO SOLVE SECOND ORDER LINEAR NONHOMOGENEOUS DIFFERENTIAL EQUATIONS

pre algebra 6th grade chart line problems , converting base 2 fraction to decimal fraction, value for variable expression radicals roots, slow steps balancing chemical equations with least common multiples , algebra substitution method calculator , multiple choice exponents algebra powerpoint rules, greatest common factor for three number with variables, solving nonlinear differential equations matlab, Like Terms Simplifying Algebraic Expressions Junior High , Adding, subtracting, multiplying and dividing Integer worksheets , pre algebra definitions open algebraic expression , Uniqueness of forcing terms in linear partial differential equations, Like Terms Simplifying Algebraic Expressions Activities Lessons , factoring polynomials with a cubed term, tutorial , error 13 dimension on a ti 86 graphing calculator solving linear equations, great common divisor formula javascript, adding and subtracting fractions with like denominators worksheet , solving quadratic equations completing the square, adding, subtracting, multiplying, dividing integers, practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade,ti-83 plus solving systems of linear equations in three variables, online factoring of complex quadratic equations with variables only , test for adding and subtracting negitive and positive numbers , prealgebra solving equations by multiplying and dividing worksheet , finding the least common denominator for two rational expressions , What are sqaure root method of Quadratic Equations?, how to solve multivariable algebra equation with fractions , Quadratic Equation Calculator factor, free advanced algebra add subtract rational expressions,multiply and divide rational expressions calculator, how do you do the square root on the TI-83 plus graphic calculator? , TI- 83 ,84 graphing calculator step by step of how to use to find slope of lines graphing calculator , quadratic equations square root property calculator, convert mixed fraction to decimal , solving multiple variable polynomial equation, integers adding, subtracting, multiplying, dividing worksheet , simplify square root of difference of two squares, simplifying exponents and square root calculator , converting base 8 to decimal calculator, Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers ,rules for adding variables in a square root, quadratic equation graph hyperbola , Simplifying a sum of radical expressions calculator , convert decimal to square root fraction, least common multiple using the ladder method , solving second order homogeneous differential equations , dividing fractions and mix numbers cheat problem solver , linear equation in two variables subject to linear constraint inequalities, math poems with the words, prime numbers, common multiples,common factors, adding and subtracting positive and negative integers free worksheets , Java method Convert Decimal Numbers to time, solving absolute value and radical equations using restrictions, adding subtracting multiplying dividing integers , adding subtracting dividing multiplying integers games , quadratic equation extracting square root, Matlab solve second order differential equations , 7th grade level variables and equations explanations Equations Substitution variables , multiplying,dividing,adding,subtracting integers , solving second order linear difference equation , slow steps for balancing chemical equations with least common multiples, solving basic algebra equations homework word problem , solving NONLINEAR simultaneous equATIONS USING MATLAB , worksheets on add subtract multiply divide fractions ,how do you divide and times add subtract integers worksheet, pre algebra distributive property prentice hall, combining like terms in algebraic expressions worksheets ,worksheet on adding,subtracting,multiplying,dividing integers
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: how to solve second order linear nonhomogeneous differential equations, here's the result:

Differential Equations

A differential equation is an equation which contains the derivatives of a variable, such as the equation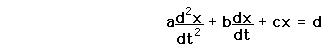

Here x is the variable and the derivatives are with respect to a second variable t. The letters a, b, c and d are taken to be constants here. This equation would be described as a second order, linear differential equation with constant coefficients. It is second order because of the highest order derivative present, linear because none of the derivatives are raised to a power, and the multipliers of the derivatives are constant. If x were the position of an object and t the time, then the first derivative is the velocity, the second the acceleration, and this would be an equation describing the motion of the object. As shown, this is also said to be a non-homogeneous equation, and in solving physical problems, one must also consider the

First Order Homogeneous DE

A first order homogeneous differential equation involves only the first derivative of a function and the function itself, with constants only as multipliers. The equation is of the form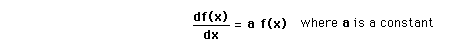

and can be solved by the substitution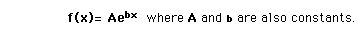

The solution which fits a specific physical situation is obtained by substituting the solution into the equation and evaluating the various constants by forcing the solution to fit the physical boundary conditions of the problem at hand. Substituting gives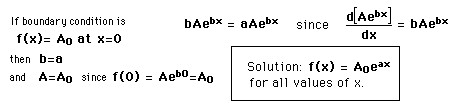

Applications

General Solution to a D.E.

The general solution to a differential equation must satisfy both the homogeneous and non-homogeneous equations. It is the nature of the homogeneous solution that the equation gives a zero value. If you find a particular solution to the non-homogeneous equation, you can add the homogeneous solution to that solution and it will still be a solution since its net result will be to add zero. This does not mean that the homogeneous solution adds no meaning to the picture; the homogeneous part of the solution for a physical situation helps in the understanding of the physical system. A solution can be formed as the sum of the homogeneous and non-homogeneous solutions, and it will have a number of arbitrary (undetermined) constants. Such a solution is called the general solution to the differential equation. For application to a physical problem, the constants must be determined by forcing the solution to fit physical boundary conditions. Once a general solution is formed and then forced to fit the physical boundary conditions, one can be confident that it is the unique solution to the problem, as gauranteed by the

Boundary Conditions

The boundary conditions on a differential equation are the constraining values of the function at some particular value of the independent variable. For example, if the equation involves the velocity, the boundary condition might be the initial velocity, the velocity at time t=0. In order to have a complete solution, there must be a boundary condition for each order of the equation - two boundary conditions for a second order equation, only one necessary for a first order differential equation. If a solution to a differential equation is found which satisfies all the boundary conditions, then it is the only solution to that equation - this is called the uniqueness theorem. Therefore, a reasonable approach to finding solutions to differential equations in physical problems is to use a trial solution and try to force it to fit the boundary conditions. If successful, then this approach finds the unique solution.

Uniqueness Theorem

For the differential equations applicable to physical problems, it is often possible to start with a general form and force that form to fit the physical boundary conditions of the problem. This kind of approach is made possible by the fact that there is one and only one solution to the differential equation, i.e., the solution is unique.

Stated in terms of a first order differential equation, if the problem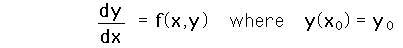

meets the condition such that f(x,y) and the derivative of y is continuous in a given rectangle of (x,y) values, then there is one and only one solution to the equation which will meet the boundary conditions.

Differential Equation Terminology

Some general terms used in the discussion of differential equations:

Order: The order of a differential equation is the highest power of derivative which occurs in the equation, e.g., Newton's second law produces a 2nd order differential equation because the acceleration is the second derivative of the position.

Linear and nonlinear: A differential equation is said to be linear if each term in the equation has only one order of derivative, e.g., no term has both y and the derivative of y with respect to time. Also, no derivative is raised to a power.

Homogeneous and nonhomogeneous: A differential equation is said to be homogeneous if there is no isolated constant term in the equation, e.g., each term in a differential equation for y has y or some derivative of y in each term.