Get it on Google Play Get it on Apple Store



EQUATION OF THE LINE SOLVER ORDERED PAIRS
solving multiple variable polynomial equation , how use my Casio Calculator for solving linear equations ,  Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers, solving second order nonlinear differential equations ,   convert decimal to fraction - formula ,     dividing algebraic terms online free calculator, converting base 2 fraction to decimal fraction ,   multiplying,dividing,adding,subtracting integers , solving second order linear difference equation ,  solving second order non-homogeneous differential equations ,   solving absolute value and radical equations using restrictions,   solving quadratic equations 3 variables,   Like Terms Simplifying Algebraic Expressions Junior High ,   Like Terms Simplifying Algebraic Expressions Activities Lessons,   free help on a 4>3 solve the inequality. graph the solutions on a number line ,   test for adding and subtracting negitive and positive numbers, HOW DO I DIVIDE A FRACTION BY A RADICAL FRACTION, value for variable expression radicals roots ,  Combining Like Terms pre-algebra worksheet ,  multiply and divide rational expressions calculator ,   how to solve multivariable algebra equation with fractions, simplify dividing algebra expressions online calculator free ,  linear equation in two variables subject to linear constraint inequalities, What are sqaure root method of Quadratic Equations? ,  practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade , find suare root of real numbers ,   adding, subtracting, multiplying, dividing integers , method to solve third order polynomials , rules for adding variables in a square root ,   online factoring of complex quadratic equations with variables only , adding subtracting multiplying and dividing integers ,   graphing linear equations on the coordinate plane powerpoint ,    slow steps for balancing chemical equations with least common multiples,   online calculator that solves complex trinomials , combining like terms powerpoint lesson ,  finding the least common denominator for two rational expressions, dividing fractions and mix numbers cheat problem solver , multi root quadratic equation solver TI-83, solving simultaneous equations with excel equation solver, math poems with the words, prime numbers, common multiples,common factors ,   simplifying exponents and square root calculator ,     how to solve exponential probability in TI-83 Plus calculator , slope solving by elimination online calculator ,    square odd integer multiple of 8 plus one triangle number , Quadratic Equation Calculator factor, simple pre-algebra equations ,     prealgebra solving equations by multiplying and dividing worksheet, solving quadratic equations by completing the square ,   solve nonlinear differential equation first order, Uniqueness of forcing terms in linear partial differential equations ,   Simplifying a sum of radical expressions calculator ,  adding subtracting dividing multiplying integers games, pre algebra adding and subtracting integers worksheet ,    help with the algebraic expression four times a number divided by three ,   integers adding, subtracting, multiplying, dividing worksheet,   fractions formula adding subtracting multiplying, worksheets on add subtract multiply divide fractions,square roots and cube roots activity ,   simplify radical expressions calculator root , Solving Non Linear Simultaneous Equations,    solve nonlinear equation system maple symbolic ,      pre algebra distributive property prentice hall ,  simplifying complex rational expressions solver,    solve my algebra problem with a calculator and fractions ,     Java method Convert Decimal Numbers to time , Adding, subtracting, multiplying and dividing Integer worksheets , free advanced algebra add subtract rational expressions,    exponents Simplifying Multiplication Expressions Lesson Plan ,   error 13 dimension on a ti 86 graphing calculator solving linear equations ,    example of pictures of plotting points on the graphing calculator ,    slow steps balancing chemical equations with least common multiples, factoring polynomials with a cubed term, tutorial, how do you divide and times add subtract integers worksheet ,  solving quadratic equations completing the square ,solving nonlinear differential equations matlab ,  Maths worksheet for highest common factor & least common factor for year 7,    algebraic formula percentage number variable , Multiplying rational expression fractions solver , solving addition and subtraction equations ,  solving third order linear equations , examples of quadratic equations with fractional exponential , greatest common factor for three number with variables ,  least common denominator calculator , solving partial differential equations by factoring ,   adding ,subtracting ,multiplying ,and dividing fractions,  worksheets solving addition and subtraction equations ,    adding and subtracting positive and negative integers free worksheets ,   quadratic equation extracting square root ,  how do you do the square root on the TI-83 plus graphic calculator? ,  solving quadratics by factoring powerpoints, solving second order nonhomogeneous differential equation, math help containing equivalent fractions decimals and percentages ,    integer problems adding multiplying dividing subtract, solving nonhomogeneous 2nd order differential equations ,  solve my algebra problem with a calculator and fractions for free ,   order of fractions from least to greatest Glencoe,McGraw-Hill,     find vertex of absolute value equations,  worksheet solving addition and subtraction equations , fraction and decimal multiplying and dividing worksheets,    simplified radical form square roots ,  how to solve first order linear differential equations using laplace transform,  convert mixed number to decimal,  how to solve second order linear nonhomogeneous differential equations, convert decimal to fraction algebra worksheet , quadratic equations square root property calculator , combining like terms in algebraic expressions worksheets,  7th grade level variables and equations explanations Equations Substitution variables ,  solving nonhomogeneous second order linear differential equation ,   techniques in getting the least common denominator in college algebra ,    multiplying dividing adding subtracting fractions , convert decimal to square root fraction , solving cubed polynomials equations ,adding and subtracting fractions with like denominators worksheet ,   ti-83 plus solving systems of linear equations in three variables ,   adding subtracting multiplying dividing integers,  solving radicals and square roots , simplify square root of difference of two squares, Algebra I help turning rational equations into linear equations , greatest common factor of two numbers is 871 , solving basic algebra equations homework word problem ,  worksheet on adding,subtracting,multiplying,dividing integers ,  solving 2nd order differential equation

Thank you for visiting our site! You landed on this page because you entered a search term similar to this: equation of the line solver ordered pairs, here's the result:

Systems of Equations
In Electronics and with Matrices
Back to Activities page
This site explores the solution of two simultaneous equations for two unknowns.

There are three different manners in which you may want to explore this site depending on your interest and needs. They can be interchanged or used by themselves.

Electronics Application of Simultaneous Linear Equations

Linear Simultaneous Equations are frequently encountered in electronics and technology. For example, when using Kirchhoff's Laws (KCL & KVL) for analyzing a circuit you eventually arrive at a system of loop equations that must be solved for CURRENTS I1 and I2. These two unknowns are solution to the network that is established by Kirchhoff's Laws.

Links to Kirchhoff's Laws

Kirchhoff's Voltage Law

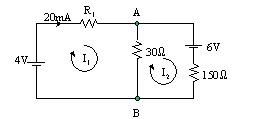
As per the diagrams to the right the SUM of the Voltage Terms in the loops should be ZERO. The three different currents are I1 , I2 and I3 with I3 = I1 + I2.

Steps to solving Kirchhoff Law Equations.

1. Consider each loop as a seperate equation with I1 &  I2 as variables to solve for.

2. Solve simultaneous equations for the unknown quantities. I1 & I2

Solving for the variables is described below.

 

Loop 1 - Loop 2 = 0

 

 

 

 

A System of Equations has one solution. This solution is a set of ordered pairs of the form (x,y) that satisfies two or more equations. A System of Equations is generally of the (standard) form. It is helpful to arrange (rewrite the equations of the system) to look like the standard form:

AX + BY = C
DX + EY = F

and one ordered pair (x,y) satisfies these two equations.

Or in electronics

AI1 + BI2 = C
DI1 + EI2 = F

and one ordered pair (I1,I2) satisfies these two equations.

Example:

Eq 1. ) 3I1 + I2 = 14
Eq 2. ) 2I1 + 3I2 = 7
The next step is to perform operations on one equation in the system to eliminate one variable and solve for the other.

Using the example, we want to find a way to make the coefficient of either I1 or I2 equal so that we can isolate the other variable and solve for it. Try multiplying the entire Eq 1. by "3" so that we have

Eq 1. ) (3)3I1+ (3)I2 = (3)14
Eq 2. ) 2I1 + 3I2 = 7
Now we have

Eq 1. ) 9I1+ 3I2 = 42
Eq 2. ) 2I1 + 3I2 = 7
We can then subtract Eq. 2 from Eq. 1 and solve for I1.

7I1 = 35

and so,

I1 = 5

Insert this I1 = 5 back into either Eq. 1 or Eq. 2 and then you will be able to solve for X.
Let's Insert it into Eq. 2.

Eq 2. ) 2I1 + 3I2 = 7
Eq 2. ) 2(5) + 3I2 = 7
Eq 2. ) 10 + 3I2 = 7
Eq 2. ) 3I2 = 7 - 10
Eq 2. ) 3I2 = -3
Eq 2. ) I2 = -1
top

 

Interactive Solver for I1 and I2

Eq 1. ) 3I1 + I2 = 14
Eq 2. ) 2I1 + 3I2 = 7

Try these Equations in the Solver below and hit the "Solve" Button.

top

Systems of Equations in terms of x and y and a SOLVER

A System of Equations has one solution. This solution is a set of ordered pairs of the form (x,y) that satisfies two or more equations. A System of Equations is generally of the (standard) form. It is helpful to arrange (rewrite the equations of the system) to look like the standard form:

AX + BY = C
DX + EY = F

and one ordered pair (x,y) satisfies these two equations.

One way to solve this system of equations is to graph both equations (make sure to set y = equation) and observe the intersection of the lines that are plotted. This intersection point is the ordered pair that represents the solution.

You can try this by hand on paper or by using a graphing utility like a graphing calculator, or even a tool available on the web.

Try this example by graphing it:

Eq 1. ) X+ 2Y = 10
Eq 2. ) 2X - Y = 10
Another method is to perform operations on one equation in the system to eliminate one variable and solve for the other.

Using the same example:

Eq 1. ) X+ 2Y = 10
Eq 2. ) 2X - Y = 10
We want to find a way to make the coefficient of either x or y equal so that we can isolate the other variable and solve for it.

Try multiplying the entire Eq 1. by "2" so that we have

Eq 1. ) (2)X+ (2)2Y = (2)10
=
Eq 1. ) 2X+ 4Y = 20
Now we have

Eq 1. ) 2X+ 4Y = 20
Eq 2. ) 2X - Y = 10
We can then subtract them and solve for Y.

5Y = 10
and so,
Y = 2
Insert this Y = 2 into either Equation and then you will be able to solve for X.

Eq 2. ) 2X - Y = 10
Eq 2. ) 2X - (2) = 10
Eq 2. ) 2X = 12
Eq 2. ) X = 6
Does this match with what you have graphed?
Try it out numerically by entering values here (remember to put "-" for a negative sign.) and then hit the "Solve" button.

top

 Solver: Just Enter your Coefficient Values and hit solve

Matrices and Cramer's Rule for Solving a System of Equations

Solutions to systems of equations of the form

AX + BY = C
DX + EY = F

Can be found using the following:
(CE - BF)

X =

(AE - BD)

(AF - CD)

Y =

(AE - BD)

This method is derived from the determinants of matrices that can be arranged from a system of equations

Recall that a matrix A is of the form

[A] =

| a

b |

| c

d |
The value of the determinant of the 2 X 2 matrix is the difference of the diagonal products.

a*d - c * b = determinant A

To solve a system of the form

AX + BY = C
DX + EY = F

1.) Find the determinants of the following matrices.

[A] =

| a

b |

| d

e |
a*e - d * b = determinant A

[Ax] =

| c

b |

| f

e |
c * e - f * b = determinant Ax

[Ay] =

| a

c |

| d

f |
a*f - d * c = determinant Ay

2.) Use the determinants to find the solution if determinant A is not zero.

X =
determinant Ax
determinant A

Y =
determinant Ay
determinant A

top

 

Illinois LearningStandards

STATE GOAL 8: Use algebraic and analytical methods to identify and describe patterns and relationships in data, solve problems and predict results.

8.D.4 Formulate and solve linear and quadratic equations and linear inequalities algebraically and investigate nonlinear inequalities using graphs, tables, calculators and computers.