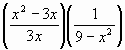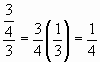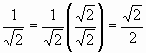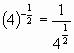Algebrator by Softmath - the leading Mathematics Software Application on the Market today! Algebra Software Tutoring Program provides exceptional supplemental teaching and reduces homework time

Home
News
Why Algebrator?
Iron-clad Guarantee
Testimonials and Reviews
Compare to Others
Order
Who we are
FAQs
Algebra Resource Links
Privacy Policy
Free tutoring with purchase!
Click here for a demo of Algebrator by SoftMath--reduce your Algebra homework to no time at all!
 

Softmath
1150 N Loop 1604 W
Ste. 108-453
San Antonio, TX 78248
USA

Phone: (512) 788-5675
Fax:     (512) 519-1805

 
BBB Reliability Program -- Algebrator by SoftMath: reduce your homework time today!

Read the review of Algebrator Software in the Family Review Center today!
Bookmark and Share
 
 

TECHNIQUES IN GETTING THE LEAST COMMON DENOMINATOR IN COLLEGE ALGEBRA

dividing fractions and mix numbers cheat problem solver,solving quadratics by factoring powerpoints,worksheet solving addition and subtraction equations,solve my algebra problem with a calculator and fractions,square odd integer multiple of 8 plus one triangle number,quadratic equations square root property calculator,solve nonlinear differential equation first order,free help on a 4>3 solve the inequality. graph the solutions on a number line,What are sqaure root method of Quadratic Equations?,dividing algebraic terms online free calculator,solving second order nonhomogeneous differential equation,exponents Simplifying Multiplication Expressions Lesson Plan,math poems with the words, prime numbers, common multiples,common factors,Simplifying a sum of radical expressions calculator,Like Terms Simplifying Algebraic Expressions Activities Lessons,adding and subtracting positive and negative integers free worksheets,least common denominator calculator,solving radicals and square roots,how to solve first order linear differential equations using laplace transform,convert mixed number to decimal,simplifying complex rational expressions solver,how to solve exponential probability in TI-83 Plus calculator,multi root quadratic equation solver TI-83,combining like terms in algebraic expressions worksheets,adding, subtracting, multiplying, dividing integers,Maths worksheet for highest common factor & least common factor for year 7,solving quadratic equations completing the square,simple pre-algebra equations,pre algebra distributive property prentice hall,simplified radical form square roots,pre algebra adding and subtracting integers worksheet,value for variable expression radicals roots,equation of the line solver ordered pairs,slope solving by elimination online calculator,Combining Like Terms pre-algebra worksheet,Adding, subtracting, multiplying and dividing Integer worksheets,prealgebra solving equations by multiplying and dividing worksheet,HOW DO I DIVIDE A FRACTION BY A RADICAL FRACTION,solving third order linear equations,solving 2nd order differential equation,multiply and divide rational expressions calculator,simplify radical expressions calculator root,integer problems adding multiplying dividing subtract,solving nonhomogeneous 2nd order differential equations,solve nonlinear equation system maple symbolic,solve my algebra problem with a calculator and fractions for free,math help containing equivalent fractions decimals and percentages,greatest common factor for three number with variables,multiplying,dividing,adding,subtracting integers,solving addition and subtraction equations,example of pictures of plotting points on the graphing calculator,examples of quadratic equations with fractional exponential,combining like terms powerpoint lesson,Multiplying rational expression fractions solver,quadratic equation extracting square root,adding subtracting multiplying and dividing integers,how use my Casio Calculator for solving linear equations,algebraic formula percentage number variable,worksheets solving addition and subtraction equations,solving nonhomogeneous second order linear differential equation,solving cubed polynomials equations,solving quadratic equations by completing the square,order of fractions from least to greatest Glencoe,McGraw-Hill,online calculator that solves complex trinomials,Java method Convert Decimal Numbers to time,fraction and decimal multiplying and dividing worksheets,solving second order nonlinear differential equations,help with the algebraic expression four times a number divided by three,solving partial differential equations by factoring,slow steps for balancing chemical equations with least common multiples,fractions formula adding subtracting multiplying,solving basic algebra equations homework word problem,7th grade level variables and equations explanations Equations Substitution variables,solving second order linear difference equation,simplifying exponents and square root calculator,linear equation in two variables subject to linear constraint inequalities,worksheets on add subtract multiply divide fractions,converting base 2 fraction to decimal fraction,factoring polynomials with a cubed term, tutorial,Algebra I help turning rational equations into linear equations,worksheet on adding,subtracting,multiplying,dividing integers,ti-83 plus solving systems of linear equations in three variables,method to solve third order polynomials,free advanced algebra add subtract rational expressions,Solving Non Linear Simultaneous Equations,how do you divide and times add subtract integers worksheet,convert decimal to fraction algebra worksheet,how to solve second order linear nonhomogeneous differential equations,Quadratic Equation Calculator factor,simplify square root of difference of two squares,solving simultaneous equations with excel equation solver,simplify dividing algebra expressions online calculator free,integers adding, subtracting, multiplying, dividing worksheet,square roots and cube roots activity,convert decimal to square root fraction,adding and subtracting fractions with like denominators worksheet,convert decimal to fraction - formula,find suare root of real numbers,how do you do the square root on the TI-83 plus graphic calculator?,find vertex of absolute value equations,adding subtracting multiplying dividing integers,Uniqueness of forcing terms in linear partial differential equations,Like Terms Simplifying Algebraic Expressions Junior High,adding ,subtracting ,multiplying ,and dividing fractions,graphing linear equations on the coordinate plane powerpoint,adding subtracting dividing multiplying integers games,practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade,multiplying dividing adding subtracting fractions,finding the least common denominator for two rational expressions,solving multiple variable polynomial equation,slow steps balancing chemical equations with least common multiples,solving absolute value and radical equations using restrictions,rules for adding variables in a square root,greatest common factor of two numbers is 871,solving nonlinear differential equations matlab,error 13 dimension on a ti 86 graphing calculator solving linear equations,test for adding and subtracting negitive and positive numbers,Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers,solving second order non-homogeneous differential equations,solving quadratic equations 3 variables,how to solve multivariable algebra equation with fractions,online factoring of complex quadratic equations with variables only
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: techniques in getting the least common denominator in college algebra, here's the result:
REVIEW/TUTORIAL FOR THE COLLEGE ALGEBRA PLACEMENT TEST
 
1. Evaluate x2 3x + 9 for x = 1
2.
Multiply and simplify:
3. Simplify and factor: 5x 2(y x) x
4.
Simplify:
5.
Simplify and write as a single fraction:
6.
Simplify as much as possible:
7.
Simplify by rationalizing the denominator:
 
8. Multiply: (8x3 y)(3x2y7)
 
9. Find the slope of the line: 2x 3y + 10 = 0
10.
Write as a single fraction in terms of
11.
Solve for all values of x:
12.
Solve for all values of x: = 5
13.
Multiply and simplify:
14. Find the solution set for x: 2x + 1 > 3x + 7
15. Solve for x: 2x2 + 3x 2 = 0
16. Solve for x: 2x2 3x 4 = 0
17. Solve for x: 2x2 6x + 5 = 0
18.
Evaluate:
19.
Solve for x and y:
20.
Find the solution set for x:
21.
Write as a single fraction.
22. Factor completely: x4 81.
23.
Add and simplify:
24. The graphs of the system of equation consists of lines that
a) intersect b) meet in one point c) are parallel
25.
Simplify:
26. Find the solution set for x: x2 + 6 > 5x
27. If f(x) = x3 + 1, find f(3)
28. Graph: y = 1
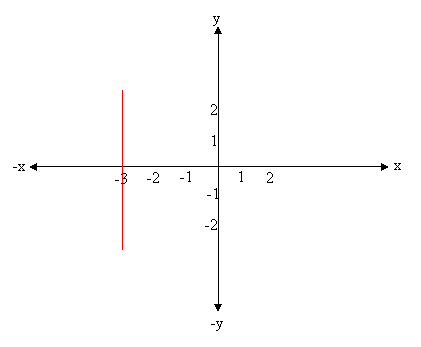
29. Graph: x = 3
30. Graph: 2x + 3y = 2

     
 
ANSWERS FOR THE REVIEW/TUTORIAL
     
1. Answer 5
Evaluate x2 3x + 9  for x = 1
When substituting x = 1 in   x2
be sure to do the exponent before the multiplication by   1
    to get    (1)2 = 1.   So     1 3 + 9 = 5
 
2. Answer
When multiplying so that
   
becomes
 
3. Answer 2(3x - y)   
    Using the distribute law -2(y - x) = -2y + 2x we get:
5x 2(y x) x
= 5x 2y + 2x x
= 6x -2y
= 2(3x - y)
 
4. Answer
To divide by 3, we invert and multiply
 
5. Answer
Write the numerator as a single fraction with denominator of 4,
    and write the denominator as a single fraction with denominator of 6,
   
   
Now divide by
Be sure to invert and multiply to get
   
Here we divided the denominator 4 and the numerator 6 by 2.
 
6. Answer
  , 
     
since x4 is positive. Similarly
 
7. Answer
Since we write
   
 
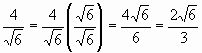8. Answer 24x5y8
When multiplying exponent expressions with the same base, keep the
    base and add the exponents thus, x3(x2) = x5 and y(y7) = y8
 
9. Answer
Write the equation of the line in the form y = mx + b or where m is the slope.
    3y = 2x 10
 
10. Answer
Write
and rationalize
Now we are adding
 
11. Answer
Multiply both sides of the equation by the denominator x 3
   
Use the fact that
1 3(x 3) = x
1 3x + 9 = x
10 = 4x
 
12. Answer x = 5,   x = 5
There are two values of x whose absolute value is 5
|-5| = 5   and   |5| = 5
     
 
13. Answer
We factor x2 3x = x(x 3)   and   9 x2 = (3 x)(3 + x)
Remember the difference of squares factorization
a2 b2 = (a b)(a + b).
    Thus we get
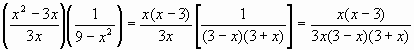Use the fact that x – 3 = – (3 – x),   so that
   
Putting this together we get
   
 
     
14. Answer x < 6
2x + 1 > 3x + 7
Subtract 3x  from both sides x + 1 > 7
Subtract 1 from both sides x > 6
Multiply by 1, we get x < 6
Remember multiplying an inequality by a minus changes the sense of the arrow.
     
15. Answer
and x = 2
Consider the standard quadratic equation ax2 + bx + c = 0,
whose solution is
For the solution of 2x2 + 3x 2 = 0, a = 2, b = 3, and c = 2.
Since the discriminant b2 4ac = 32 4(2)( 2) = 9 + 16 = 25 is a
perfect square, we can factor directly: 2x2 + 3x 2 = 0,
(2x 1)(x + 2) = 0
2x 1 = 0 x + 2 = 0
x = 2
     
16. Answer
For the solution of 2x2 3x 4 = 0, we have a = 2, b = 3, c = 4.
The discriminant b2 4ac = ( 3)2 4(2)( 4) = 9 + 32 = 41 is not a
perfect square so that we must use the quadratic formula and get
two real roots: Thus
     
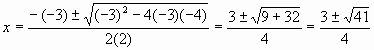17. Answer
For the solution of 2x2 6x + 5 = 0, a = 2, b = 6, c = 5
     
The discriminant b2 4ac = ( 6)2 4(2)( 5) = 36 40 = 4.
     
Since the discriminant is negative, the two roots are imaginary.
     
     
   
 
     
Thus, here we use
     
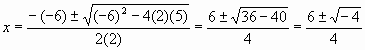We can reduce the answer by factoring 2 in the numerator
     
     
18. Answer
The negative exponent means we have to take the reciprocal of what is in
the parentheses and then square.
Remember when raising a fraction to a power, both the denominator and
numerator are raised to that power
     
19. Answer x = 3, y = 2 Solve for x and y there are two methods that are often used.
Addition method: Multiply the second equation by 5
     
5x 3y = 21
5x 25y = 35
Add the equations to get:
28y = 56
     
Substitute back into the second equation to get:
x + 5( 2) = 7
x 10 = 7
x = 7 + 10 = 3
Thus x = 3, y = 2.
     
Substitution method: Solve for x in the second equation to get:
x = 7 5y
Substitute for x in the first equation to get:
   
  5(–7 – 5y) – 3y = 21
  –35 – 25y – 3y = 21
  –35 – 28y = 21
Add 35 – 28y = 21 + 35
  – 28y = 56
  Divide by – 28
 
Substitute in equation two to get x. Substitute the value y = 2
in x = 7 5y to get x = 7 5(2) = 7 + 10 = 3
Thus x = 3, y = 2.
     
 
20. Answer Answer: 3 < x < 7
We can do the problem algebraically or geometrically.
Algebraically:
|x - 2| < 5 means 5 < x 2 < 5
So by adding to 2 all three parts of the inequality we get
5 < x 2 < 5
5 + 2 < x 2 + 2 < 5 + 2
3 < x < 7
     
Geometrically:
|x - 2| < 5 means that the distance (in both directions) from x to 2 is less than 5.
So if we move 5 units to the right (up the axis) from 2 we get 7 and 5 units
to the left (down the axis) from 2 we get 3
     
 
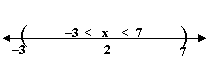21. Answer
The least common denominator is xy. Thus
Since the denominators of the two fractions are now the same,
we can add the numerators getting
     
     
22. Answer (x 3)(x +3)(x2 + 9)
Recall the factorization of the difference of squares a2 b2 = (a b)(a + b)
x4 81 is a difference of squares namely (x2 )2 and 92.
x4 81 = (x2 9)( x2 + 9). The first factor is again a difference of squares:
(x2 9) = (x 3)(x +3)
x4 81 = (x2 9)( x2 + 9) = (x 3)(x +3)(x2 + 9)
x2 + 9, the sum of squares, does not factor
     
 
23. Answer
The least common denominator is 24y.
Thus
Here since the denominators are the same we add the numerator.
     
 
24. Answer The lines are parallel.
If you solve for y in each equation to get the form y = mx + b,
you can examine the slopes m and the y intercepts b.
Equation 1 becomes:
Equation 2 becomes:
which reduces to
   
Since the slopes are equal and the y intercepts are not, the lines are
parallel. In the case that both the slopes and the y intercepts were equal,
    the lines would be the same.
    In the case that the slopes are unequal, the lines intersect in one point.
     
 
25. Answer 2
Think of as as
     
is the cube root of 8 often written as
     
   
So that
     
the meaning of a negative exponent.
     
   
is the square root of 4
     
often written Thus
     
 
26. Answer x < 2  or  x > 3
x2 5x + 6 > 0
To find the solution set for x set the inequality equal to zero and factor and solve for x:
x2 5x + 6 = 0
(x 3)(x 2) = 0
x = 3, x = 2
Since the inequality is strictly greater than zero, neither of these are in the solution set.
These two numbers divide the x axis into three sections:
     
¥ < x < 2, 2 < x < 3, and 3 < x < ¥
     
Pick any "test" number for each section and substitute into the inequality:
     
For ¥ < x < 2, say x = 0.
     
Substituting x = 0 into x2 5x + 6 gives us (0)2 5(0) + 6 = 6
    which is greater than zero.
     
Thus ¥ < x < 2 is part of the solution set.
For 2 < x < 3, we can test with or
   
Substituting into x2 5x + 6  gives us
which is less than zero.
     
Thus 2 < x < 3, is NOT in our solution set.
For 3 < x < ¥, we can substitute x = 4   to get
    42 5(4) +6 = 16 20 + 6 = 12 > 0.
Thus 3 < x < ¥ is part of the solution set.
Thus the complete solution set is {x| ¥ < x < 2 or 3 < x < ¥}
which can also be written in interval notation as ( ¥, 2) (3, ¥).
     
27. Answer 28
If f(x) = x3 + 1, f(3) = 33 + 1 = 28
     
 
28. Answer The horizontal line one unit above the x axis.
29. Answer The vertical line 3 units to the left of the y axis.
     
     
30. Answer The graph of  2x + 3y = 2   is
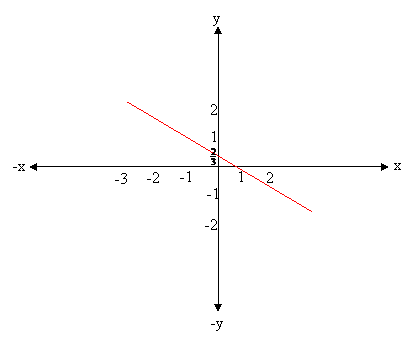To graph 2x + 3y = 2, we need to find any two points which lie on the line
and connect them with the straight edge. There are several ways to do this.
    We outline two common methods.
Intercept method:
     
If we let x = 0, the y intercept is 3y = 2 or
    and if we let y =0 the x intercept is (1,0)
     
Slope-Intercept method:
     
Solving for y in the form y = mx + b we get:
From this form we see that the y intercept is
From this point we can use the slope, which is
    to find a second point by moving, 2 units to the left (0 2 = 2)
   
and 3 units up to get the second point
     
Close

You Type in Your Algebra Problem. Algebrator does the Rest!

 

Algebrator
Download (and optional CD)

Only $39.99

Click to Buy Now:



OR

Goods and services provided by Sofmath (TX, USA).
Sold by 2CheckOut.com Inc. (Ohio, USA).

Attention: We are currently running a special promotional offer for softmath.com visitors -- if you order Algebrator by midnight of November 7th you will pay only $39.99 instead of our regular price of $74.99 -- this is 35.00 in savings ! In order to take advantage of this offer, you need to order by clicking on one of the buttons on the left, not through our regular order page.

If you order now you will also receive 30 minutes of live math tutoring from tutor.com!

You Will Learn Algebra Better - Guaranteed!

Just take a look how incredibly simple Algebrator is:

Step 1 : Enter your homework problem in an easy WYSIWYG (What you see is what you get) algebra editor:

Step 2 : Let Algebrator solve it:

Step 3 : Ask for an explanation for the steps you don't understand:

Algebrator can solve problems in all the following areas:

  • simplification of algebraic expressions (operations with polynomials (simplifying, degree, synthetic division...), exponential expressions, fractions and roots (radicals), absolute values)
  • factoring and expanding expressions
  • finding LCM and GCF
  • operations with complex numbers (simplifying, rationalizing complex denominators...)
  • solving linear, quadratic and many other equations and inequalities (including basic logarithmic and exponential equations)
  • solving a system of two and three linear equations (including Cramer's rule)
  • graphing curves (lines, parabolas, hyperbolas, circles, ellipses, equation and inequality solutions)
  • graphing general functions
  • operations with functions (composition, inverse, range, domain...)
  • simplifying logarithms
  • operations with matrices (adding, subtracting, multiplying, inverse...)
  • basic geometry and trigonometry (similarity, calculating trig functions, right triangle...)
  • arithmetic and other pre-algebra topics (ratios, proportions, measurements...)

Algebrator
Download (and optional CD)

Only $39.99

Click to Buy Now:



OR

Goods and services provided by Sofmath (TX, USA).
Sold by 2CheckOut.com Inc. (Ohio, USA).

 
Order $58.99
 

 

 
 
Demo | Features | Guarantee | Reviews | Comparison | Order | About Us

©Copyright 1998 - 2009 Softmath All rights reserved.