dividing algebraic terms online free calculator, solving second order linear difference equation , how do you divide and times add subtract integers worksheet , 7th grade level variables and equations explanations Equations Substitution variables , solving second order non-homogeneous differential equations , HOW DO I DIVIDE A FRACTION BY A RADICAL FRACTION ,   integers adding, subtracting, multiplying, dividing worksheet ,   factoring polynomials with a cubed term, tutorial, solve my algebra problem with a calculator and fractions for free , least common denominator calculator, finding the least common denominator for two rational expressions ,  solving second order nonhomogeneous differential equation ,   Maths worksheet for highest common factor & least common factor for year 7 ,  solving quadratic equations 3 variables, ti-83 plus solving systems of linear equations in three variables ,  solving multiple variable polynomial equation ,   Solving Non Linear Simultaneous Equations, worksheet solving addition and subtraction equations , adding subtracting dividing multiplying integers games,Like Terms Simplifying Algebraic Expressions Activities Lessons , simplify dividing algebra expressions online calculator free , value for variable expression radicals roots ,  linear equation in two variables subject to linear constraint inequalities ,   worksheet on adding,subtracting,multiplying,dividing integers , multi root quadratic equation solver TI-83, convert decimal to square root fraction, order of fractions from least to greatest Glencoe,McGraw-Hill , Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers ,   adding, subtracting, multiplying, dividing integers,  solving absolute value and radical equations using restrictions ,    example of pictures of plotting points on the graphing calculator, prealgebra solving equations by multiplying and dividing worksheet , worksheets on add subtract multiply divide fractions,  simplify radical expressions calculator root , rules for adding variables in a square root , adding and subtracting fractions with like denominators worksheet ,  solving quadratic equations completing the square , adding subtracting multiplying dividing integers,  multiplying dividing adding subtracting fractions, Quadratic Equation Calculator factor,  multiplying,dividing,adding,subtracting integers ,   solving third order linear equations,  math help containing equivalent fractions decimals and percentages ,   pre algebra distributive property prentice hall, integer problems adding multiplying dividing subtract ,   free advanced algebra add subtract rational expressions ,  simplifying complex rational expressions solver, adding ,subtracting ,multiplying ,and dividing fractions,how use my Casio Calculator for solving linear equations ,   simplified radical form square roots, Uniqueness of forcing terms in linear partial differential equations ,  solve my algebra problem with a calculator and fractions ,   solving 2nd order differential equation,   error 13 dimension on a ti 86 graphing calculator solving linear equations , solving partial differential equations by factoring , convert decimal to fraction - formula , Java method Convert Decimal Numbers to time , simplifying exponents and square root calculator,  greatest common factor of two numbers is 871, greatest common factor for three number with variables , Algebra I help turning rational equations into linear equations ,  solving nonlinear differential equations matlab ,   how to solve multivariable algebra equation with fractions ,  online calculator that solves complex trinomials , help with the algebraic expression four times a number divided by three ,  how do you do the square root on the TI-83 plus graphic calculator?,    Multiplying rational expression fractions solver , practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade, Adding, subtracting, multiplying and dividing Integer worksheets , simplify square root of difference of two squares ,   online factoring of complex quadratic equations with variables only,    combining like terms powerpoint lesson ,fraction and decimal multiplying and dividing worksheets,  math poems with the words, prime numbers, common multiples,common factors , solving simultaneous equations with excel equation solver , how to solve first order linear differential equations using laplace transform ,   convert mixed number to decimal , solving radicals and square roots , find vertex of absolute value equations , quadratic equation extracting square root ,   Simplifying a sum of radical expressions calculator,   slope solving by elimination online calculator,  worksheets solving addition and subtraction equations ,solving nonhomogeneous second order linear differential equation , solving cubed polynomials equations,  Like Terms Simplifying Algebraic Expressions Junior High , free help on a 4>3 solve the inequality. graph the solutions on a number line , multiply and divide rational expressions calculator ,     how to solve second order linear nonhomogeneous differential equations , solve nonlinear equation system maple symbolic,  examples of quadratic equations with fractional exponential, pre algebra adding and subtracting integers worksheet ,   quadratic equations square root property calculator , square roots and cube roots activity,    find suare root of real numbers,  graphing linear equations on the coordinate plane powerpoint , What are sqaure root method of Quadratic Equations? , adding and subtracting positive and negative integers free worksheets ,  algebraic formula percentage number variable , adding subtracting multiplying and dividing integers, solving quadratics by factoring powerpoints ,   test for adding and subtracting negitive and positive numbers,  solving quadratic equations by completing the square,    techniques in getting the least common denominator in college algebra,   solving second order nonlinear differential equations , solve nonlinear differential equation first order , slow steps for balancing chemical equations with least common multiples ,     slow steps balancing chemical equations with least common multiples ,     fractions formula adding subtracting multiplying , square odd integer multiple of 8 plus one triangle number , method to solve third order polynomials ,  solving basic algebra equations homework word problem,converting base 2 fraction to decimal fraction ,   simple pre-algebra equations,   exponents Simplifying Multiplication Expressions Lesson Plan , Combining Like Terms pre-algebra worksheet ,  solving nonhomogeneous 2nd order differential equations ,    how to solve exponential probability in TI-83 Plus calculator ,  dividing fractions and mix numbers cheat problem solver ,  convert decimal to fraction algebra worksheet , equation of the line solver ordered pairs ,  combining like terms in algebraic expressions worksheets
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving addition and subtraction equations.We have an extensive database of resources on solving addition and subtraction equations. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter! 

---

Addition/Subtraction Method for Solving Systems of Two Equations Algebraically manipulate both equations so that all the variables are on one side of the equal sign and in the same order. (Line the equations up, one on top of the other.) If needed, multiply one of the equations by a constant so that there is one variable in each equation that has the same coefficient. Subtract one equation from the other. Solve the resulting equation for the one variable. (Use the technique described in previous units.) Using the value found in the step 4, substitute it into either equation and solve for the remaining variable. Substitute the values for both variables into the equation not used in step 5 to be sure our solution is correct.

While there seems to be a lot of steps to this process, itreally is rather simple. Let’s work through one example tosee how the steps work. We have two equations below:

P = 2 + 2Q
P = 10 – 6Q

To solve for the numeric value of each variable, we shouldfollow the steps outlined above.

1. Algebraically manipulate both equationsso that all the variables are on one side of the equal sign andin the same order. (Line the equations up, one on top of the other.)

When we do this we get the equations shown at the right. Notice how the terms containing P are lined up, as are the terms containing Q.

P – 2Q = 2 P + 6Q = 10

2. If needed, multiply one of the equationsby a constant so that there is one variable in each equation thathas the same coefficient.

The variable P in both equations has a coefficient ofone, so we move on to the next step.

3. Subtract one equation from the other.

 

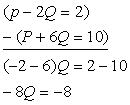
4. Solve the resulting equation for the one variable.

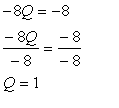
5. Using the value found in the step4, substitute it into either equation and solve for the remainingvariable.

   In the previous step we found that Q = 1. We plug this value back into either of our initial equations and solve for P.

   P = 2 + 2Q P = 2 + 2(1) P = 4

   6. Substitute the values for both variablesinto the equation not used in step 5 to be sure our solution iscorrect.

      Now we substitute the value of Q = 1 and P = 4 into the equation not used in step 5.

      P = 10 – 6Q 4 = 10 – 6(1) 4 = 4.

      These values work in this equation so we have the correct answer.

      Keep in mind that you can use either method for solving systemsof equations. Let’s revisit the example we used in the lastsection, but this time solve it using addition/subtraction.

      Example
      Solve the system of linear equations given below usingaddition/subtraction.

      Suppose there is a piggybank that contains 57 coins, whichare only quarters and dimes. The total number of coins in thebank is 57, and the total value of these coins is $9.45. Thisinformation can be represented by the following system of equations:

      D + Q = 57
      0.10D + 0.25Q = 9.45

      Determine how many of the coins are quarters and how many aredimes.

      Answer
      The information in this example can be represented by the followingsystem of equations:

      D + Q = 57
      0.10D + 0.25Q = 9.45

      Determine how many of the coins are quarters and how many are dimes.

      D = 32 (number of dimes) Q = 25 (number of quarters)

      Detailed Answer
      We were given the two equations:

      D + Q = 57     (1)
      0.10D + 0.25Q = 9.45     (2)

      1. Algebraically manipulate both equationsso that all the variables are on one side of the equal sign andin the same order.

      When we do this we get the equations shown at the right. Notice how the terms containing D are lined up, as are the terms containing Q.

      D + Q = 57 0.10D + 0.25Q = 9.45

      2. If needed, multiply one of the equationsby a constant so that there is one variable in each equation thathas the same coefficient.

      Because neither of the variables has the same coefficient inboth equations, we will need to multiply one equation by a numberthat will result in the variable in one equation having the samecoefficient as in the other. In this example we can see the coefficientof Q in equation (1) is 4 times larger than the coefficient ofQ in equation (2).

      If we multiply the second equation by 4, then the variable Q will have the same coefficient in both equations. This means that both sides of equation (2) must be multiplied by 4.

      0.10D + 0.25Q = 9.45 4(0.10D + 0.25Q = 9.45) 4(0.10)D + 4(0.25)Q = 4(9.45) 0.40D + 1Q = 37.8

      3. Subtract one equation from the other. Now we subtract one equation from the other.

      D + Q = 57
      - (0.40D + Q = 37.8)
      0.60D = 19.2

      4. Solve the resulting equation for theone variable.

      We now solve the equation from step 3 to find a value for the D variable.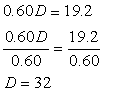

      5. Using the value found in the step4, substitute it into either equation and solve for the remainingvariable.

      Now we substitute the value of D = 32 into one of the equations to solve for Q.

      D + Q = 57 32 + Q – 32= 57 – 32 Q = 25

      6. Substitute the values for both variablesinto the equation not used in step 5 to be sure our solution iscorrect.

      Now we substitute the value of D = 32 and Q = 25 into the equation not used in step 5.

      0.10D + 0.25Q = 9.45 .10(32) + .25(25) = 9.45 3.20 + 6.25 = 9.45 9.45 = 9.45

      So we find that Q = 25 and D = 32. If you lookback at the last section you will find this is the same resultwe found then.

      If you wish to try a practice problem now, return to the introductionand select the practice or additional practice button.