Get it on Google Play Get it on Apple Store



SIMPLIFIED RADICAL FORM SQUARE ROOTS
slow steps balancing chemical equations with least common multiples, solving nonhomogeneous 2nd order differential equations ,    multiply and divide rational expressions calculator , prealgebra solving equations by multiplying and dividing worksheet , solving third order linear equations ,   how to solve exponential probability in TI-83 Plus calculator ,  equation of the line solver ordered pairs ,  convert decimal to square root fraction , Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers , solving multiple variable polynomial equation,  Adding, subtracting, multiplying and dividing Integer worksheets ,    fraction and decimal multiplying and dividing worksheets , fractions formula adding subtracting multiplying, simplify radical expressions calculator root ,  how do you do the square root on the TI-83 plus graphic calculator? ,     worksheet solving addition and subtraction equations ,  value for variable expression radicals roots , multiplying,dividing,adding,subtracting integers,   worksheets on add subtract multiply divide fractions,   Like Terms Simplifying Algebraic Expressions Activities Lessons,  rules for adding variables in a square root , solving second order non-homogeneous differential equations,  adding and subtracting positive and negative integers free worksheets,    graphing linear equations on the coordinate plane powerpoint,   solve nonlinear equation system maple symbolic ,   error 13 dimension on a ti 86 graphing calculator solving linear equations ,  test for adding and subtracting negitive and positive numbers,   finding the least common denominator for two rational expressions ,   order of fractions from least to greatest Glencoe,McGraw-Hill , multi root quadratic equation solver TI-83 , multiplying dividing adding subtracting fractions , how to solve first order linear differential equations using laplace transform ,  converting base 2 fraction to decimal fraction ,   solving cubed polynomials equations,  Quadratic Equation Calculator factor ,    slow steps for balancing chemical equations with least common multiples,   Multiplying rational expression fractions solver , practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade,   square roots and cube roots activity , free advanced algebra add subtract rational expressions , simplify square root of difference of two squares , solving simultaneous equations with excel equation solver , how do you divide and times add subtract integers worksheet ,  how to solve second order linear nonhomogeneous differential equations ,   method to solve third order polynomials,   Like Terms Simplifying Algebraic Expressions Junior High ,solving second order nonhomogeneous differential equation,   HOW DO I DIVIDE A FRACTION BY A RADICAL FRACTION , convert decimal to fraction algebra worksheet , math help containing equivalent fractions decimals and percentages ,   find suare root of real numbers ,  linear equation in two variables subject to linear constraint inequalities ,   free help on a 4>3 solve the inequality. graph the solutions on a number line ,   simplifying complex rational expressions solver ,   combining like terms powerpoint lesson, adding, subtracting, multiplying, dividing integers, Solving Non Linear Simultaneous Equations, solving 2nd order differential equation,  slope solving by elimination online calculator , integers adding, subtracting, multiplying, dividing worksheet ,  solve my algebra problem with a calculator and fractions for free , solving quadratic equations 3 variables,  solving nonhomogeneous second order linear differential equation ,   Algebra I help turning rational equations into linear equations , solving partial differential equations by factoring ,   What are sqaure root method of Quadratic Equations?, greatest common factor for three number with variables ,  algebraic formula percentage number variable ,    dividing algebraic terms online free calculator ,   solve my algebra problem with a calculator and fractions ,    example of pictures of plotting points on the graphing calculator , quadratic equations square root property calculator ,   simplify dividing algebra expressions online calculator free,   online factoring of complex quadratic equations with variables only ,  solving quadratics by factoring powerpoints,   online calculator that solves complex trinomials ,   pre algebra adding and subtracting integers worksheet , how use my Casio Calculator for solving linear equations ,  ti-83 plus solving systems of linear equations in three variables,   adding subtracting dividing multiplying integers games , convert decimal to fraction - formula, worksheet on adding,subtracting,multiplying,dividing integers,  Maths worksheet for highest common factor & least common factor for year 7 ,   least common denominator calculator,    solving second order nonlinear differential equations ,pre algebra distributive property prentice hall , simplifying exponents and square root calculator ,  techniques in getting the least common denominator in college algebra,    solving second order linear difference equation ,     help with the algebraic expression four times a number divided by three ,  solving radicals and square roots ,   simple pre-algebra equations ,   Simplifying a sum of radical expressions calculator, integer problems adding multiplying dividing subtract,   quadratic equation extracting square root, solving addition and subtraction equations , adding ,subtracting ,multiplying ,and dividing fractions ,    math poems with the words, prime numbers, common multiples,common factors ,    how to solve multivariable algebra equation with fractions,    solving basic algebra equations homework word problem , factoring polynomials with a cubed term, tutorial, convert mixed number to decimal ,   solving quadratic equations completing the square, solving nonlinear differential equations matlab,  adding and subtracting fractions with like denominators worksheet ,  dividing fractions and mix numbers cheat problem solver , combining like terms in algebraic expressions worksheets , solving quadratic equations by completing the square , solving absolute value and radical equations using restrictions ,   adding subtracting multiplying and dividing integers , solve nonlinear differential equation first order , greatest common factor of two numbers is 871 ,  Java method Convert Decimal Numbers to time ,   exponents Simplifying Multiplication Expressions Lesson Plan , Combining Like Terms pre-algebra worksheet ,   square odd integer multiple of 8 plus one triangle number ,find vertex of absolute value equations , Uniqueness of forcing terms in linear partial differential equations , worksheets solving addition and subtraction equations ,  adding subtracting multiplying dividing integers , examples of quadratic equations with fractional exponential , 7th grade level variables and equations explanations Equations Substitution variables
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: simplified radical form square roots, here's the result:

Intermediate Algebra
Tutorial 41:
Rationalizing Denominators andNumerators 
of Radical Expressions


Learning Objectives

 
After completing this tutorial, you should be able to:
  1. Rationalize one term denominators of rational expressions.
  2. Rationalize one term numerators of rational expressions.
  3. Rationalize two term denominators of rational expressions.

 
 
 
Introduction

 
In this tutorial we will talk about rationalizing the denominator andnumerator of rational expressions.  Recall from Tutorial3: Sets of Numbers that a rational number is a number that canbe written as one integer over another. Recall from Tutorial3: Sets of Numbers that an irrational number is not one that ishard to reason with but is a number that cannot be written as one integerover another.  It is a non-repeating, non-terminating decimal. Oneexample of an irrational number is when you have a root of an expressionthat is not a perfect root, for example, the square root of 7 or the cuberoot of 2.  So when we rationalize either the denominator or numeratorwe want to rid it of radicals.  Hopefullyyou will not encounter too many irrational numbers in your life as Frankand Ernest do, but just in case you do, we will help you be prepared forthat moment.

 
 
Tutorial

 
 
Rationalizing the Denominator 
(with one term)

 
When a radical contains an expression that is not a perfect root,for example, the square root of 3 or cube root of 5,  it is calledan irrational number. So, in order to rationalizethe denominator, we need to get rid of all radicals that are in the denominator.

 
 
Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the denominator.

 
If the radical in the denominator is a square root, then you multiplyby a square root that will give you a perfect square under the radicalwhen multiplied by the denominator.   If the radical in the denominatoris a cube root, then you multiply by a cube root that will give you a perfectcube under the radical when multiplied by the denominator and so forth...

Note that the phrase "perfect square" meansthat you can take the square root of it.  Just as "perfectcube" means we can take the cube root of the number, and soforth. 

Keep in mind that as long as you multiply the numerator and denominatorby the exact same thing, the fractions will be equivalent.


 
Step 2: Make sureall radicals are simplified.

 
Some radicals will already be in a simplified form, but make sure yousimplify the ones that are not.  If you need a review on this,

 
Step 3: Simplify the fraction if needed.

 
Be careful.  You cannot cancel out a factor that is on the outsideof a radical with one that is on the inside of the radical.  In orderto cancel out common factors, they have to be both inside the same radicalor be both outside the radical.

 
 
Example1:   Rationalize the denominator .

 
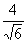Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the denominator.

 
Since we have a square root in the denominator, then we need tomultiply by the square root of an expression that will give us a perfectsquare under the radical in the denominator.

Square roots are nice to work with in this type of problem because ifthe radicand is not a perfect square to begin with, we just have to multiplyit by itself and then we have a perfect square.

So in this case we can accomplish this by multiplying top and bottomby the square root of 6:


 

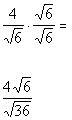*Mult. num. and den. by sq. root of 6
 
 

*Den. now has a perfect square under sq. root
 


 
Step 2: Make sureall radicals are simplified

AND


 
Step 3: Simplify the fraction if needed.

 

 
 

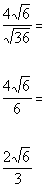*Sq. root of 36 is 6
 
 

*Divide out the common factor of 2
 


 
Be careful when you reduce a fraction like this.  It is real temptingto cancel the 3 which is on the outside of the radical with the 6 whichis inside the radical on the last fraction.  You cannot do that unlessthey are both inside the same radical or both outside the radical likethe 4 in the numerator and the 6 in the denominator were in the secondto the last fraction. 

 
 
 
Example2:   Rationalize the denominator .

 
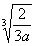Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the denominator.

 
Since we have a cube root in the denominator, we need to multiplyby the cube root of an expression that will give us a perfect cube underthe radical in the denominator. 
 

So in this case, we can accomplish this by multiplying top and bottomby the cube root of :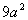


 

 

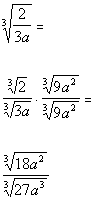*Mult. num. and den. by cube root of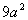 
 
 
 

*Den. now has a perfect cube under cube root

 


 
Step 2: Make sureall radicals are simplified

AND


 
Step 3: Simplify the fraction if needed.

 

 

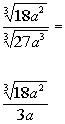*Cube root of 27 acube is 3a

 


 
As discussed in example 1, we would not be able to cancel out the 3with the 18 in our final fraction because the 3 is on the outside of theradical and the 18 is on the inside of the radical. 

Also, we cannot take the cube root of anything under the radical. So, the answer we have is as simplified as we can get it.


 
 
 
Rationalizing the Numerator
(with one term)

 
As mentioned above, when a radical cannot be evaluated,  forexample, the square root of 3 or cube root of 5,  it is called anirrationalnumber.  So, in order to rationalizethe numerator, we need to get rid of all radicals that are in the numerator.

Note that these are the same basic steps forrationalizing a denominator, we are just applying to the numerator now.


 
 
Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the numerator.

 
If the radical in the numerator is a square root, then you multiplyby a square root that will give you a perfect square under the radicalwhen multiplied by the numerator.   If the radical in the numeratoris a cube root, then you multiply by a cube root that will give you a perfectcube under the radical when multiplied by the numerator and so forth...

Note that the phrase "perfect square" meansthat you can take the square root of it.  Just as "perfectcube" means we can take the cube root of the number, and soforth. 

Keep in mind that as long as you multiply the numerator and denominatorby the exact same thing, the fractions will be equivalent.


 
Step 2: Make sureall radicals are simplified.

 
Some radicals will already be in a simplified form, but make sure yousimplify the ones that are not.  If you need a review on this,

 
Step 3: Simplify the fraction if needed.

 
Be careful.  You cannot cancel out a factor that is on the outsideof a radical with one that is on the inside of the radical.  In orderto cancel out common factors, they have to be both inside the same radicalor be both outside the radical.

 
 
 
Example3:   Rationalize the numerator .

 
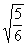Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the numerator.

 
Since we have a square root in the numerator, then we need to multiplyby the square root of an expression that will give us a perfect squareunder the radical in the numerator. 

So in this case, we can accomplish this by multiplying top and bottomby the square root of 5:


 

 

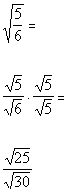*Mult. num. and den. by sq. root of 5
 
 

*Num. now has a perfect square under sq. root

 


 
Step 2: Make sureall radicals are simplified.

AND


 
Step 3: Simplify the fraction if needed.

 

 

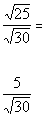*Sq. root of 25 is 5

 


 
As discussed above, we would not be able to cancel out the 5 with the30 in our final fraction because the 5 is on the outside of the radicaland the 30 is on the inside of the radical. 

Also, we cannot take the square root of anything under the radical. So, the answer we have is as simplified as we can get it.


 
 
 
Example4:   Rationalize the numerator .

 
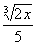Step 1: Multiply numerator and denominator by a radicalthat will get rid of the radical in the numerator.

 
Since we have a cube root in the numerator,  we need to multiplyby the cube root of an expression that will give us a perfect cube underthe radical in the numerator. 

So in this case, we can accomplish this by multiplying top and bottomby the cube root of :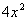


 

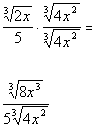*Mult. num. and den. by cube root of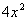 
 
 

*Num. now has a perfect cube under cube root

 


 
Step 2: Make sureall radicals are simplified

AND


 
Step 3: Simplify the fraction if needed.

 

 

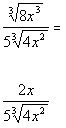*Cube root of 8 x cubeis 2x

 


 
As discussed above, we would not be able to cancel out the 2xwith the 4 x squared in our final fraction,because the 2x is on the outside of the radicaland the 4 x squared is on the inside of theradical. 

Also, we cannot take the cube root of anything under the radical. So, the answer we have is as simplified as we can get it.


 
 
Rationalizing the Denominator 
(with two terms)

 
Above we talked about rationalizing the denominator with one term. Again, rationalizing the denominator means to get rid of any radicals inthe denominator. 

Because we now have two terms, we are going to have to approach it differentlythan when we had one term, but the goal is still the same.


 
Step 1: Find the conjugate of the denominator.

 
You find the conjugate of a binomial by changing the sign that is betweenthe two terms, but keep the same order of the terms. 

a + band a - b are conjugatesof each other.


 
Step 2: Multiply the numerator and the denominatorof the fraction by the conjugate found in Step 1 .

 
Keep in mind that as long as you multiply the numerator and denominatorby the exact same thing, the fractions will be equivalent.

 
Step 3: Make sureall radicals are simplified.

 
Some radicals will already be in a simplified form, but make sure yousimplify the ones that are not.  If you need a review on this,

 
Step 4: Simplify the fraction if needed.

 
Be careful.  You cannot cancel out a factor that is on the outsideof a radical with one that is on the inside of the radical.  In orderto cancel out common factors, they have to be both inside the same radicalor be both outside the radical.

 
 
 
Example5:   Rationalize the denominator 

 
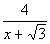Step 1: Find the conjugate of the denominator.

 
In general the conjugate of a + bisa- b and vice versa.

So what would the conjugate of our denominator be?

It looks like the conjugate is .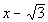


 
Step 2: Multiply the numerator and the denominatorof the fraction by the conjugate found in Step 1.

 

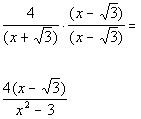*Mult. num. and den. by conjugate of den.
*Productof the sum and diff. of two terms
 
 

 


 
Step 3: Make sureall radicals are simplified

AND


 
Step 4: Simplify the fraction if needed.

 
No simplifying can be done on this problem so the final answer is: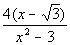


 
 
 
 
Example6:   Rationalize the denominator .

 
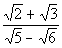Step 1: Find the conjugate of the denominator.

 
In general the conjugate of a + bisa- b and vice versa.

So what would the conjugate of our denominator be?

It looks like the conjugate is .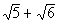


 
Step 2: Multiply the numerator and the denominatorof the fraction by the conjugate found in Step 1 .

 
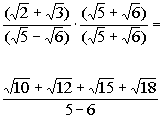*Mult. num. and den. by conjugate of den.
*Use FOILmethod in num.
*Productof the sum and diff. of two terms
 

 


 
Step 3: Make sureall radicals are simplified

AND


 
Step 4: Simplify the fraction if needed.

 

 

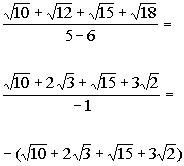*12 is (4)(3) and sq. root of 4 is 2
*18 is (9)(2) and sq. root of 9 is 3
 
 

 


 
 
 
Practice Problems

 
These are practice problems to help bring you to the next level. It will allow you to check and see if you have an understanding of thesetypes of problems. Math works just like anythingelse, if you want to get good at it, then you need to practice it. Even the best athletes and musicians had help along the way and lots ofpractice, practice, practice, to get good at their sport or instrument. In fact there is no such thing as too much practice.

To get the most out of these, you should work the problem out onyour own and then check your answer by clicking on the link for the answer/discussionfor that  problem.  At the link you will find the answeras well as any steps that went into finding that answer.


 

PracticeProblem 1a:

Rationalize the Denominator.


 
 
1a.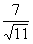 
(answer/discussionto 1a)

 


 

PracticeProblem 2a:

Rationalize the Numerator.


 
 
2a.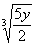 
(answer/discussionto 2a)


 
 

PracticeProblem 3a:

Rationalize the Denominator.


 
 
3a.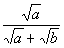 
(answer/discussionto 3a)

 
 
 
Need Extra Help on These Topics?

 
 
No appropriate web pages could be found tohelp you with the topics on this page. 
 
 

for somemore suggestions.


 


All contents
Jan. 8, 2002