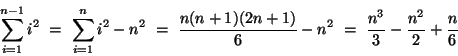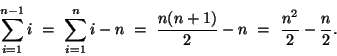Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving third order linear equations, here's the result:
| Even though computers are becoming faster and more powerful, eachcomputation (an addition or a multiplication, for example) that a computer performs takes a finite amount of time.If the solution of a particular problem requires too many of theseindividual computations, the computer time needed to solve it may very well exceed the time the user has available to work on the problem -- and in some cases the time required may exceed theuser's lifetime. The solution of a linear system is one of the most frequentlyperformed calculations in computational mathematics.Some problems can be modeled directly as a linear system.Others have a different form, but require the solution oflinear systems as a part of their solution.Solving some of these problems requires solution of thousands oflinear systems; and each linear system may contain thousands ofequations. In order to compare the four methods defined in Chapter 2, we will count the number of algebraic operations that each performs. When we discuss the cost of a particular method, we are referring to the number of algebraic operations that the computer must perform in order to obtain a solution. Thus, the methods that we deem “inefficient” or “expensive” compared with the others simply require more algebraic operations. As we present the cost of the methods in terms of n, the size of the system, notice whether or not the cost increases significantly as we increase n. Also, keep in mind that multiplication and division operations are generally more expensive than addition and subtraction operations because they are more time consuming for the computer. Addition and subtraction take almost the same amount of time, so they are customarily grouped together. When counting operations the “addition” count includes both addition and subtraction operations. Similarly, the “multiplication” count includes both multiplication and division.
We will determine the cost of Gaussian Elimination by counting the number of addition and multiplication operations that must be performed. Forward elimination and back substitution will be considered separately. Let's consider first a 3 x 3 example. 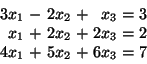 The steps involved in Gaussian Elimination are shown below: 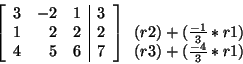 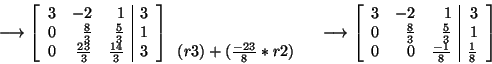 First, we will count the number of arithmetic operations required to eliminate all of the zeros below the first element in the first column of the coefficient matrix. In order to introduce a zero in the first position of the second row, we had to compute the constant by which we would multiply the first row. We did this by dividing, but we will refer to the calculation as a multiplication when doing the operation count. Next we multiplied the second, third, and right-hand-side elements of row one by In the second step, we used the second row to eliminate the second element in the third row. We multiplied the third and right-hand-side elements of row 2 by This completes the forward elimination phase. The operation count so far is:
Now let's consider the back substitution phase.Starting from the bottom of the final augmented matrix, we compute the value of x3 by dividing the right-hand-sideelement of row 3 by the third element in row 3.This requires 1 multiplication. Substituting the value of x3 into the second equation requiresmultiplying its value by 2.So we require one more multiplication.Using the second row to solve for x2 requires subtracting 4x3 from the right-hand-side element of row 3and then dividing the result by the third element.This requires 1 addition and 1 multiplication.All together, calculation of x2 requires 2 multiplications and 1 addition. Finally, substituting both x3 and x2 into the first equation requires 2 multiplications, and solving the first equation forx1 requires 2 additions and 1 multiplication.Hence calculation of x1 requires 3 multiplications and 2additions. In summary, the steps in back substitution for our 3 x 3 system required
1 + 2 + 3 = multiplications and
0 + 1 + 2 = 3 additions The complete count for Gaussian Elimination on this system is thus 28 operations: 17 multiplications and 11 additions. Nothing in this count depended on the particular coefficient matrix or right-hand side appearing in the problem. Gaussian Elimination for any 3 x 3 linear system will require the same number of operations. Now we would like to extend this process to linear systems of other sizes. Since we don't want to have to handle each possible problem size individually, we will consider a general n x n system. The n x (n + 1) augmented matrix for the system has the following form:  In the first step of Gaussian elimination, we introduce zeros in all the positions in the first column below the diagonal element, a11. To do this, we first compute the constant by which we need tomultiply the first row in order to introduce a zero in thefirst element of row 2.Then we multiply the last n elements in the first row by a this constant and then add the result to the second row. This requires n+1 multiplications and n additions.Remember that we do not actually compute the zeros below the diagonal, so we do not have to consider any of the elements in column one when doing the count.Notice that one multiplication and one addition came from operations on the right-hand-side element of the row.Later, we will be interested in modifying this number in orderto determine the operation count for problems with multipleright-hand sides. Introducing zeros in the first position of any of the lower rows will require multiplication by a different constant, but the number of multiplications and additions will be the same as for row two. Hence the first step of Gaussian Elimination requires n+1 multiplications and n additions for each of the n-1 rows below row one. The total is (n-1)(n+1) multiplications and (n-1)(n) additions. At the end of the first step, the elements of rows below the first will have changed. We indicate this by denoting the elements by a'ij. 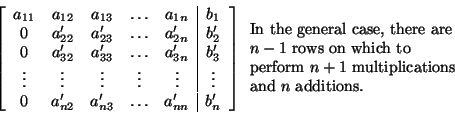 Now that we have zeros in the first column, we wish to introduce zeros below the diagonal element, a'22, in the second column. Since the zeros in the first column will not affect any additional row operations, we only have to perform n multiplications and n-1 additions on the third through nth rows of our matrix to achieve elimination in the second column. So the operation count for step two is (n-2)(n) multiplications and (n-2)(n-1) additions. 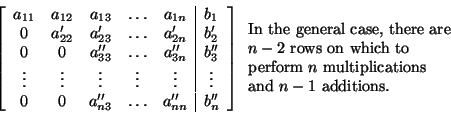 Considering the first two steps together, we get (n-1)(n+1) + (n-2)(n) multiplications and (n-1)(n) + (n-2)(n-1) additions. We continue eliminating elements below the diagonals for columns three through n-2. The last step in the forward elimination process is to introduce zeros below the diagonal element in the (n-1)st column of the matrix. Again, we will disregard the zeros, so only 1 multiplication for computing the contstant, 2 multiplications by this constant on the (n-1)st row, and the addition of the last two elements of the (n-1)st and nth rows are required. Hence that last step requires 3 multiplications and 2 additions. After the last or (n-1)st step, we have the matrix 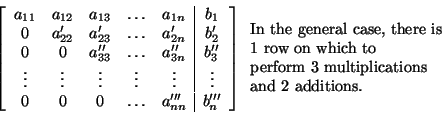 The total operation count for the forward elimination phase ofGaussian Elimination is
Since there is a pattern in these expressions, we suspect that there might be a more compact way to write them. First, let's consider the number of multiplications. Each term consists of two factors multiplied together, and the second factor is two larger than the first. That is, each term has the form i(i+2). We can use summation notation to express the fact that the terms are added together. The summation starts at i=1 and ends at i = n - 1. So we can express the number of multiplications as 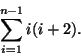 Using some of the properties of sums, we can write 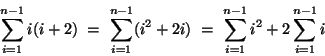 Expressions for the sum of the first n integers and the sum of thesquares of the first n integers are known: 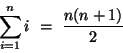 and 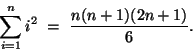 So we will rewrite our expressions to take advantage of this information.
and
Then our expression for the number of multiplications required forforward elimination is 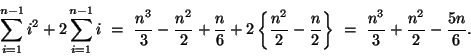 Using similar arguments, we can write the number of additions required for forward elimination as Now let's consider back substitution. The first step (row n) requires 1 multiplication and no additions; the second (row n -1) requires 2 multiplications and 1 addition. By the time we reach row 1, we need to perform n multiplications and n-1 additions. So back substitution requires
Using the expression for the sum of the first n integers, we canwrite this as Gaussian Elimination for a n x n linear system consists of forward elimination and back substitution and requires a total of |