Get it on Google Play Get it on Apple Store



SOLVING RADICALS AND SQUARE ROOTS
find suare root of real numbers, solving addition and subtraction equations , solve my algebra problem with a calculator and fractions for free,  Like Terms Simplifying Algebraic Expressions Junior High , graphing linear equations on the coordinate plane powerpoint , simplify radical expressions calculator root ,  adding subtracting multiplying and dividing integers , order of fractions from least to greatest Glencoe,McGraw-Hill , exponents Simplifying Multiplication Expressions Lesson Plan,   slow steps balancing chemical equations with least common multiples,    online factoring of complex quadratic equations with variables only ,  Maths worksheet for highest common factor & least common factor for year 7 , solving second order linear difference equation ,    solving absolute value and radical equations using restrictions,    solving partial differential equations by factoring ,  error 13 dimension on a ti 86 graphing calculator solving linear equations , Combining Like Terms pre-algebra worksheet ,  math help containing equivalent fractions decimals and percentages , Simplifying a sum of radical expressions calculator,   square roots and cube roots activity , how to solve first order linear differential equations using laplace transform , combining like terms powerpoint lesson ,   math poems with the words, prime numbers, common multiples,common factors, Quadratic Equation Calculator factor, solving second order nonlinear differential equations, free advanced algebra add subtract rational expressions ,  worksheets on add subtract multiply divide fractions,     convert decimal to fraction algebra worksheet ,    worksheet on adding,subtracting,multiplying,dividing integers , finding the least common denominator for two rational expressions, solving nonlinear differential equations matlab, fraction and decimal multiplying and dividing worksheets , Like Terms Simplifying Algebraic Expressions Activities Lessons ,how use my Casio Calculator for solving linear equations ,    method to solve third order polynomials , adding, subtracting, multiplying, dividing integers , greatest common factor of two numbers is 871 ,   solving basic algebra equations homework word problem ,   simplified radical form square roots,  practice worksheets on adding, subtracting,multiplying,and dividing decimals. for 6th grade ,    integers adding, subtracting, multiplying, dividing worksheet ,  ti-83 plus solving systems of linear equations in three variables ,   7th grade level variables and equations explanations Equations Substitution variables , Pre-Algebra chapter 2 evaluate expressions, worksheet triangle expressions answers , find vertex of absolute value equations , fractions formula adding subtracting multiplying ,  how to solve exponential probability in TI-83 Plus calculator,  solving nonhomogeneous second order linear differential equation ,    solving quadratics by factoring powerpoints , prealgebra solving equations by multiplying and dividing worksheet ,    examples of quadratic equations with fractional exponential , Adding, subtracting, multiplying and dividing Integer worksheets , value for variable expression radicals roots , solving third order linear equations, Solving Non Linear Simultaneous Equations,   free help on a 4>3 solve the inequality. graph the solutions on a number line ,    solve nonlinear differential equation first order ,   solving multiple variable polynomial equation , solving 2nd order differential equation ,   dividing fractions and mix numbers cheat problem solver ,  worksheets solving addition and subtraction equations , rules for adding variables in a square root ,  simplify dividing algebra expressions online calculator free , example of pictures of plotting points on the graphing calculator ,  converting base 2 fraction to decimal fraction , adding subtracting dividing multiplying integers games,   factoring polynomials with a cubed term, tutorial ,    pre algebra distributive property prentice hall , how do you do the square root on the TI-83 plus graphic calculator? , adding ,subtracting ,multiplying ,and dividing fractions,    algebraic formula percentage number variable,  solve my algebra problem with a calculator and fractions,    multiplying dividing adding subtracting fractions, how to solve multivariable algebra equation with fractions,   slope solving by elimination online calculator , solving simultaneous equations with excel equation solver, Uniqueness of forcing terms in linear partial differential equations ,   techniques in getting the least common denominator in college algebra , test for adding and subtracting negitive and positive numbers , slow steps for balancing chemical equations with least common multiples , least common denominator calculator,  solving nonhomogeneous 2nd order differential equations , convert decimal to fraction - formula , solving quadratic equations by completing the square,  quadratic equations square root property calculator , solving quadratic equations 3 variables, What are sqaure root method of Quadratic Equations? , equation of the line solver ordered pairs ,  linear equation in two variables subject to linear constraint inequalities ,     integer problems adding multiplying dividing subtract , simplifying exponents and square root calculator , adding and subtracting fractions with like denominators worksheet ,    simple pre-algebra equations,   how do you divide and times add subtract integers worksheet, solving cubed polynomials equations ,simplify square root of difference of two squares,combining like terms in algebraic expressions worksheets,   solve nonlinear equation system maple symbolic ,  solving second order nonhomogeneous differential equation , multiplying,dividing,adding,subtracting integers , solving second order non-homogeneous differential equations , simplifying complex rational expressions solver, help with the algebraic expression four times a number divided by three ,  adding subtracting multiplying dividing integers, square odd integer multiple of 8 plus one triangle number , Java method Convert Decimal Numbers to time , convert mixed number to decimal, Algebra I help turning rational equations into linear equations , online calculator that solves complex trinomials ,   adding and subtracting positive and negative integers free worksheets ,  quadratic equation extracting square root ,    multiply and divide rational expressions calculator ,   pre algebra adding and subtracting integers worksheet ,  how to solve second order linear nonhomogeneous differential equations,    HOW DO I DIVIDE A FRACTION BY A RADICAL FRACTION, dividing algebraic terms online free calculator ,convert decimal to square root fraction ,multi root quadratic equation solver TI-83 ,   greatest common factor for three number with variables , solving quadratic equations completing the square ,  Multiplying rational expression fractions solver ,worksheet solving addition and subtraction equations

Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving radicals and square roots, here's the result:

College Algebra
Answer/Discussion to PracticeProblems
on Radical Equations and 
Equations Involving RationalExponents


 

Answer/Discussionto 1a


 
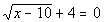
Step 1:  Isolateone of the radicals. 

 

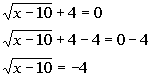*Inverse of add. 4 is sub. 4

*Square root is by itself on one side of eq.


 
Step 2: Getrid of your radical sign.

 
If you square a square root, it will disappear.  This is whatwe want to do here so that we can get x outfrom under the square root and continue to solve for it.

 
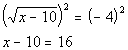*Inverse of taking the sq. root is squaringit

 
Step 3: If youstill have a radical left, repeat steps 1 and 2.

 
No more radicals exist, so we do not have to repeat steps 1 and 2.

 
Step 4: Solvethe remaining equation. 

 
In this example the equation that resulted from squaring both sidesturned out to be a linear equation.

If you need a review on solving linear equations, feel free to . 


 

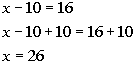*Inverse of sub. 10 is add. 10
 

 
Step 5:  Checkfor extraneous solutions.

 
Lets check to see if x = 26 is an extraneoussolution:

 

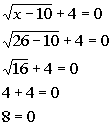*Plugging in 26 for x
 

*False statement


 
Since we got a false statement, x =26 is an extraneous solution.

There is no solution to this radical equation.


 


 

Answer/Discussionto 1b


 
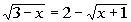
Step 1:  Isolateone of the radicals. 

 
The radical in this equation is already isolated.

 
Step 2: Getrid of your radical sign.

 
If you square a square root, it will disappear.  This is whatwe want to do here so that we can get y outfrom under the square root and continue to solve for it.

 
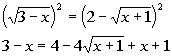*Inverse of taking the sq. root is squaringit

*Right side is a binomialsquared


 
Be careful on this one.  Itis VERY TEMPTING to square the right side term by term and get  4+ (x + 1).  However, you need to squareit as a side as shown above.  Recall that when you square a binomialyou get the first term squared minus twice the product of the two termsplus the second term squared.  If you need a review on squaring abinomial, feel free to .

 
Step 3: If youstill have a radical left, repeat steps 1 and 2.

 

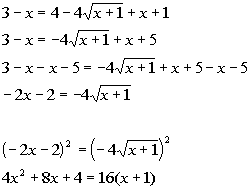*Inverse of add. xand 5 is sub. x and 5
 

*Square root is by itself on one side of eq.
 

*Inverse of taking the sq. root is squaringit
*Left side is a binomialsquared
 


 
Be careful on this one.  Itis VERY TEMPTING to square the left side term by term and get  4xsquaredplus 4.  However, you need to square it as a side as shown above. Recall that when you square a binomial you get the first term squared plustwice the product of the two terms plus the second term squared. If you need a review on squaring a binomial, feel free to .

 
Step 4: Solvethe remaining equation. 

 
In this example the equation that resulted from squaring both sidesturned out to be a quadratic equation.

If you need a review on solving quadratic equations feel free to


 

 
 
 

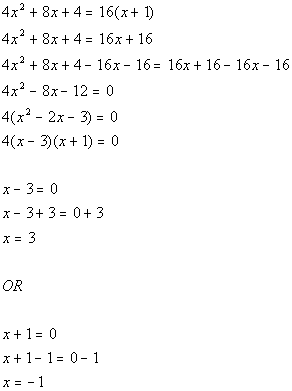*Quad. eq. in standard form
*
*Set 1st factor = 0 and solve
 
 
 
 
 

*Set 2nd factor = 0 and solve
 

 


 
Step 5:  Checkfor extraneous solutions.

 
Lets check to see if  x = 3 isan extraneous solution:

 

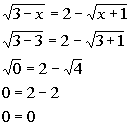*Plugging in 3 for x
 
 

*True statement


 
Since we got a true statement, x = 3is a solution.

 
Lets check to see if x = -1 is an extraneoussolution:

 

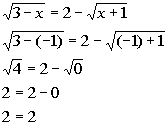*Plugging in -1 for x
 
 

*True statement


 
Since we got a true statement, x = -1is a solution.

There are two solutions to this radical equation: x= 3 and x = -1.


 


 

Answer/Discussionto 2a


 
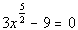
Step 1:  Isolatethe base with the rational exponent.

 
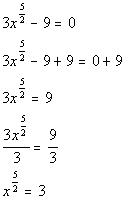*Inverse of sub. 9 is add. 9
 

*Inverse of mult. by 3 is div. by 3
 

*rat. exp. expression is by itself on one sideof eq.


 
Step 2: Getrid of the rational exponent. 

 
If you raise an expression that has a rational exponent to the reciprocalof that rational exponent, the exponent will disappear.   Thisis what we want to do here so that we can get xout from under the rational exponent and continue to solve for it.

 

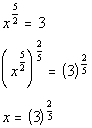*Inverse of taking it to the  5/2 poweris 
taking it to the 2/5 power

 
Step 3: Solvethe remaining equation. 

 
In this example the equation that resulted from raising both sidesto the 2/5 power turned out to be a linear equation.

Also note that it is already solved for x. So we do not have to do anything on this step for this example.


 
Step 4:  Checkfor extraneous solutions.

 
Lets check to see if 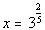is an extraneous solution:

 

 

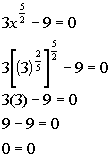*Plugging in 3 to the 2/5 power for x
 
 

*True statement


 
Since we got a true statement, 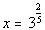isa solution.

There is one solution to this rational exponent equation: .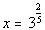


 


 

Answer/Discussionto 2b


 
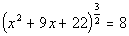
Step 1:  Isolatethe base with the rational exponent.

 
The base with the rational exponent is already isolated.

 
Step 2: Getrid of the rational exponent. 

 
If you raise an expression that has a rational exponent to the reciprocalof that rational exponent, the exponent will disappear.   Thisis what we want to do here so that we can get xout from under the rational exponent and continue to solve for it.

 

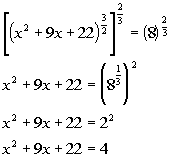*Inverse of taking it to the 3/2 power is 
taking it to the 2/3 power

*Use def.of rat. exp
 

 


 
Step 3: Solvethe remaining equation. 

 
In this example the equation that resulted from squaring both sidesturned out to be a quadratic equation.

If you need a review on solving quadratic equations, feel free to


 

 

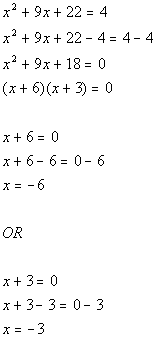*Quad. eq. in standard form
*Factorthe trinomial

*Use Zero-ProductPrinciple
*Set 1st factor = 0 and solve
 
 
 
 
 

*Set 2nd factor = 0 and solve

 


 
Step 4:  Checkfor extraneous solutions.

 
Lets check to see if x = -6 is an extraneoussolution:

 

 

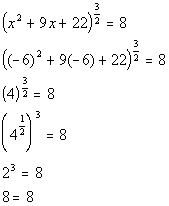*Plugging in -6 for x
 
 
 
 
 

*True statement


 
Since we got a true statement, x = -6is a solution.

 
 
Lets check to see if x = -3 is an extraneoussolution:

 
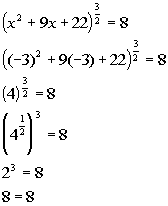*Plugging in -3 for x
 
 
 
 
 

*True statement


 
Since we got a true statement, x = -3is a solution.

There are two solutions to this rational exponent equation: x= -6 and x = -3.


 

 


All contents
July 9, 2002